附录1：激光高斯光束的传播特点

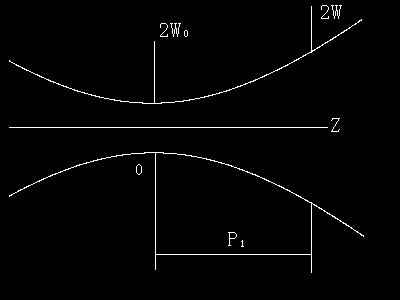
本实验中用长250毫米的内腔式氦氖激光器，其波长为632.8nm。其出射的激光束如果正入射在一块白色屏幕上所形成的光强分布是高斯分布，如图1所示，这种光束称为高斯光束。由于高斯分布的特点是光强为0的位置距光斑中心为无穷远，所以定义光强降低到中心光强的13.5%(=e^-2)时的圆环半径称为高斯光束的光斑半径W（半宽度）。高斯光束在空气中传播时其光场的等振幅线在沿光路方向为双曲线，如图2所示。因此高斯光束在传播空间用一个位置光斑最细（叫做光斑的束腰）W₀，这一位置称为高斯光束的束腰位置。根据高斯光束在空气中传播的公式可以知道：

             (1)

                  (2)

其中α=λ/πW₀²，r(Z)为高斯光束在距离束腰Z处的波面曲率半径。在该处光场的复振幅分布为：

             (3)

 

附录2：激光高斯光束通过毛玻璃后形成的散斑场的自相关函数的推导

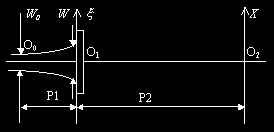
光路原理图

O₁x轴位于毛玻璃的前表面上（O₁h轴垂直纸面向外），O₂X轴位于观察平面（即为CCD的接受平面,O₂Y轴垂直纸面向外）上。激光高斯光束从激光器射出，沿光轴O₀(O₁)O₂方向入射到毛玻璃上，其束腰位置为O₀，束腰半径为W₀，从O₀到O₁x位置的距离等于P1从O₁x位置到O₂X位置的距离等于P2，由附录1公式(3)可知高斯光束到达毛玻璃平面上时其光强分布的表达式为：

             (1)

 

以下省略因子exp(j2pZ₀/l)，因为这项对光强大小无影响。设毛玻璃为无吸收位相物体，其位相分布为F(x，h)，当它表面的起伏远远大于一个波长且在一个可以分辨的小区域中包含很多的起伏的结构时，可以用狄拉克函数来表示毛玻璃上任意两点的关系：

                               (2)

 

〈〉表示系综平均。由于F(x)为平稳随机过程，所以在具体实验中(2)式总是成立的。当激光束从毛玻璃后表面透射出来，光场的复振幅用下式来描述：

                                                                               (3)

 

由菲涅尔衍射公式可以计算出此光场再传播一段距离P₂到达观察屏上的光场的复振幅分布：

                         (4)

                  (5)

 

定义μ(x₁ , y₁ ; x₂ , y₂)为复相干系数：

                                          (6)

其中^*代表复共轭，<I>表示散斑场光强的平均值，利用d函数的筛选性质完成统计平均和积分运算就可以得到

                                                            (7)

其中Dｘ=|ｘ₁-ｘ₂| ， Dｙ=|ｙ₁-ｙ₂ |，S与W的关系式为:

                                                                                                      (8)

 

附录3：关于毛玻璃移动前后两个散斑场的互相关函数与毛玻璃位移量的关系的公式

可以证明：

而且X和Y的结果在形式上完全相同。所以为了计算比较简单起见，以下我们用一维的方式进行演算。

                       (1)

 

当毛玻璃沿x移动一个小量d_0x，则可以肯定在观察屏上的光场的复振幅分布将发生变化，

                   (2)

 

所以在观察屏上由毛玻璃发生移动而产生的两个光场（即散斑场）的光强分别为：

移动前，

                                                                   (3)

移动后，

                                                                (4)

由这两个光强分布求得它们的互相关函数。由散斑统计的原理[5]可知，U₂(x₁),U₂^’(x₁),U₂(x₂)和U₂^’(x₂)是联合圆对称复高斯随机变量，故有：

                     (5)

下面令

                                                        (6)

将(1)、(2)式代入(6)并求统计平均和积分，由概率论公式和d函数的筛选性质(与附录2完全相同)，经运算得：

       (7)

因为

                   (8)

将(7)式代入(8)式得到m_c (Dx,Dy)的具体表达式，

 

其中高斯函数半宽度为S=lP₂/pW（即散斑的统计平均半宽度），高斯函数的峰值位置为

½Dx½=d_0x（1+ P₂/r（P₁））

½Dy½=d_0h（1+ P₂/r（P₁））

 

附录4：经过透镜的高斯光束束腰位置和大小的推导

 

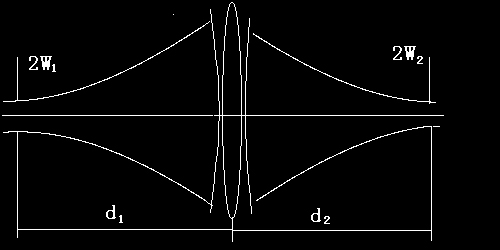
设Z₁ 为 高斯光束束腰W₀₁ 到透镜的距离，由近轴条件下高斯光束在介质中的传播规律—ABCD定律[11]可知：

                                           (1)

这里q 表示激光束的复曲率半径：

                    (2)

 

式中r(Z)表示高斯光束波面的曲率半径，W(Z)表示高斯光束的半宽度。

实验中到达透镜表面的高斯光束的波面的复曲率半径为：

                          (3)

 

经过透镜后变换为新的高斯光束的束腰位置在透镜后方距离为Z₂ 处，在此处波面的复曲率半径为：

                    (4)

 

其中A=1-Z₂/f ，B= Z₂ ，C=-1/f ，D=1。将A、B、C和D的值代入（4）式，并比较等式两边的实部和虚部的值就可以求出透镜后高斯光束的束腰位置和大小的理论值：

                             (5)

                                     (6)

其中       ，   。

利用ABCD定律也可以推导出经过透镜的高斯光束束腰位置和大小的公式，设d₁为高斯光束束腰W₀₁到透镜的距离，由ABCD定律可以推导得到经过透镜后高斯光束束腰W₀₂和高斯光束束腰W₀₂ 到透镜的距离d₂。

 

（以上内容的详细推导请参见潘笃武等编《光学》上册，p312-330，复旦大学出版社）

 

附录5：实验数据处理及误差的计算公式和方法

为了简明起见用一维函数的形式说明：

n        由CCD的每一个像元采集到像元所在位置的光强值a(i) ,i=1，2，……，N₀。得到激光散斑场的光强分布情况(如正文图2所示)。为了求出散斑半宽度的统计平均值，我们采用求a(i)的自相关函数的方法[5]。公式为：

                                     (1)

其中N=N₀-l，l=0,1,¼,L_max 。实验得到的自相关函数的形式用公式表达如下：

                              (2)

Dx=lds，ds =0.014mm 表示每一个像元的大小。a,b为小于1的常数(由实验值确定)。实验得到的自相关函数的曲线如图1所示。通过拟合就可以求出散斑半宽度的统计平均值S。

n        拟合的具体方法如下：将(2)式中右边的常数a移到左边，然后两边取对数， 得到下式：

                                 (3)

令ln(G_a(l)-a) = y，A = lnb，(3)式可以化为y = A+Bl²的形式。B = -1/S²，l=0,1,¼,L_max。于是(3)式就可以按最小二乘法进行拟合。(这里较困难的问题是a的数值的确定，目前采用的是取实验曲线的第一极小点或第一拐点。在本实验中对于满足深随机屏[3]的毛玻璃一般情况下都可以得到较好的拟合效果。)

n        互相关函数G_C(l)的实验曲线的表达式如下：

                 (4)

可以通过寻找最大值的方法找到峰值位置D，也可以按上面类似的方法进行拟合求出散斑的半宽度S(因为拟合较自相关函数的实验曲线困难，所以本文不采用) 。峰值位置D = Dx = d₀ (1+ P₂/ r(P₁) )。由于d₀和P₂为已知的实验值故可以得到r(P₁)的值。

n        由正文公式(9)可以求出r(P₁)的误差值，由正文公式S=lP2/pW(P₁)求出W(P₁)，将r(P₁)和W(P₁)的值代入正文公式(4)和(5)就可以求出高斯光束的束腰位置P₁和W₀₂。测量误差也可以利用以上三个公式推出。

 

附录6：《激光散斑测量》操作说明

[计算机开机操作：先开显示屏，后开主机电源。关机严格按操作步骤进行，主机自动关机后，再关显示屏。]

n        光路调整和光路参数测量：

按补充讲义图1排好光路(与图略有不同的是少了一个反射镜)。打开激光电源，利用散斑在透镜焦点处最大的特点找到激光束腰的位置，记下相对位置。然后将毛玻璃移动至距CCD大约**cm 的地方，测量毛玻璃距激光束腰P1和毛玻璃距CCD的距离P2。

n        计算机操作步骤：

1. 打开CCD的电源，双击计算机显示器桌面上的月亮形10Moons的图标，打开采集程序，点击“系统设置”按钮，再点击“高级设置”按钮，将“LOGO”左边的□中的对勾点掉。点击“OK”，这时黑窗口左上方的几个字母会消失。

2. 调节双偏振片，减弱激光光强到最弱，打开CCD盖子，就可以在屏幕上看到当前的散斑图像。旋转偏振片就可以看到一个清晰的亮度适中的散斑图像。

3. 按“快照”按钮，采集下一幅BMP格式的图像(大约200×200像素)。

4. 移动毛玻璃上的千分尺，大约5小格(约0.0?mm)，再采集一幅BMP格式的图像，然后可以从相册中看到拍摄的两幅BMP图像。

5. 关闭采集卡的应用程序“10Moons…”。

6. 双点击桌面上“散斑图集”，重新命名BMP图像文件名(由于采集程序自动给的名字是按时间—年月日分秒，太长)，如“w1.bmp”。把这两文件复制到F盘上

7. 进行数据处理：打开F盘。

a.      双击“读单图的程序”，输入图像文件名:如F:/w1.bmp 再输入数据文件名如F:/w1.d。

b.        双击“计算自相关函数程序”，输入数据文件名，输入Lx_max、Ly_max的值(如10，20，30，…根据散斑的大小定)输入要存盘的自相关函数的名字，如F:/w1.g1 。

c.      双击“自相关拟合程序“，输入要拟合的自相关函数的名字，，输入估计的散斑半径的值(如20)，计算机将给出S(mm)的值。

d.      双击“读双图的程序”， 输入图像文件名，再输入数据文件名等。

e.      双击“计算互相关函数”应用程序 ,输入数据文件的名字，输入要计算的图的大小X_max、Y_max (注意:要输入小于200的数据)，输入互相关函数X、Y方向最大的自变量的取值Lx_max、 Ly_max(要求输入大于散斑移动的像素个数的值)。注意:这个计算要化几分钟时间，以上输入的数据越大，计算的时间就越长，输入要保存的互相关函数的名字，如F:/w12.g2(可以用Word打开)。

f.      双击“互相关寻峰程序”，输入要寻峰的互相关函数的名字。F:/w12.g2，计算机就给出了散斑位移量DX。

在计算机处理数据时，如果确定不要采集数据了可以先关掉CCD电源。本实验要求做三组数据(不改变光路参数只要移动毛玻璃)。

 

附录7：思考题答案

1.        答:主要根据测量相关函数的统计精度的要求:由前面的理论分析可以知道，N₀(采样点总数)越大，实验的相关函数越接近理论的相关函数，但实际实验中N₀不可能无穷大，因此，在测量中要尽可能做到在CCD 的像面上有较多的散斑，同时在每一个散斑包括尽可能多的CCD像素。由于CCD的分辨率是有限的，因此必须选择合理的光路参数P₁和P₂来满足上述要求。

2.        答:由公式，所以对进行误差分析，可以知道W的测量不确定度为

因为(大约小5000倍)所以对P₂的测量精度要求远远低于对散斑颗粒度测量的要求。故可以用卷尺测量就可以了。

3.        答:略(详见正文)

4.        答:由公式，可以得到 。所以当<>时，P₂=4579mm.。

5.        答:都不会发生变化。只要CCD采样的周期小于激光器光强的起伏的周期。

6.          答:没有影响。因为均匀的背景光只影响光强的平均值。对于归一化的相关函数的值没有影响。