上机作业题

 

程序1  编写程序计算下列向量范数

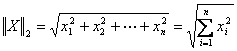                    或 

       

输入：向量的阶数，向量的元素

输出：向量范数

 

程序2  编写程序计算下列矩阵范数

    

         

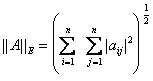
输入：方程组的阶数，矩阵的元素

输出：矩阵范数

 

程序3  编写程序计算如下级数，要求误差小于

 

并计算的值

输入：无

输出：的值

 

程序4 下面给出美国从1920年到1970年的人口表：

年份

1920

1930

1940

1950

1960

1970

人口（千人）

105711

123203

131669

150697

179323

203212

用表中数据构造一个5次拉格朗日插值多项式，并用此估计1910，1965和2002年的人口。在1910年的实际人口约为91772000，请判断插值计算得到的1965年和2002年的人口数据准确性是多少？

 

程序5 数据同上表，用牛顿插值估计：

（1）1965年的人口数；

（2）2002年的人口数。

 

程序6 数据同上表，用自然样条函数预测在1910，1965和2002年的人口数。请比较以上三种方法所求值的效果。那一种方法最优？

 

程序7 给定个插值节点，构造次拉格朗日插值多项式，并计算。

输入：插值节点数，插值点；要计算的函数点。

输出：的值。

 

程序8 对函数

                      

以如下两组节点为插值节点构造插值函数，

  （1）

  （2）

并用式子

        

对估计两组节点的误差

输入：无。

输出：两组节点对应的误差。

 

程序9 用牛顿插值构造埃尔米特插值。

输入：插值节点数，插值点；要计算的函数点。

输出：的值。

 

程序10    给定个插值点和一阶导数的端点值，用关系式构造三次样条插值多项式，求在给定点处的值。

输入：插值点数，插值点；一阶导数的端点值，要计算的函数点。

输出：的值。

 

程序11    用复化辛普森自动控制误差方法计算积分。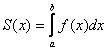

输入：积分区间，精度控制值，定义函数。

输出：积分值。

 

程序12 计算积分：

（1）      （2）

算法：计算以为积分区间的积分序列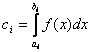，直到小于给定精度时停止。例如：积分区间序列取：

输入：积分区间序列，精度控制值，定义函数。

输出：积分值。

 

程序13  用复化Simpson积分和复化梯形积分计算

                          

取积分节点为,并对比较两种方法的误差。

输入：无

输出：两种方法对每组节点的误差。

 

程序14 用二次多项式函数拟合下列数据。并计算均方误差。

 

-2     -2.5     -2     0     1 .2      2.5     2.9

 

4.52     2.17     3.46    0    -1.39    -2.76    -5.11

输入：拟合数据序列

输出：二次多项式拟合函数，均方误差。

 

程序15  按最小二乘原理求形如 的拟合曲线。用程序9的数据，并计算均方误差。

输入：拟合数据序列

输出：拟合曲线，均方误差。

 

程序16  求解矛盾方程 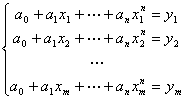 ，其中

      求解矛盾以方程组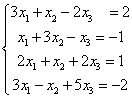  

输入：方程组的阶数，系数矩阵的元素和常向量的元素。

输出：方程组的近似解，误差。

 

程序17   用牛顿迭代法求解非线性方程组

取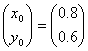，误差控制。

输入：初始点，精度控制值，定义函数。

输出：迭代次数，第步的迭代解。

 

程序18 用高斯消元法计算的行列式。

输入：行列式的阶数，行列式的元素。

输出：的行列式的值。

 

程序19 用高斯列主元消元法求解线性方程组

输入：方程组的阶数，矩阵的元素和常向量的元素。

输出：方程组的解。

 

程序20 用多利特尔直接分解法求解线性方程组。

输入：方程组的阶数，矩阵的元素和常向量的元素。

输出：方程组的解。

 

程序21 用库朗列主元直接分解法求解线性方程组。

输入：方程组的阶数，矩阵的元素和常向量的元素。

输出：方程组的解。

 

程序22 用多利特尔或库朗直接分解法求解三对角方程组：

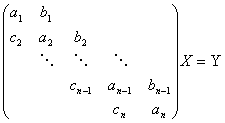
输入：方程组的阶数，从1到，常向量Y的元素。

输出：方程组的解。

 

程序23  用库朗直接分解法求解五对角方程组：

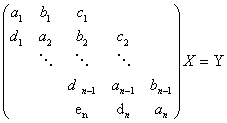
输入：方程组的阶数，从1到，常向量Y的元素。

输出：方程组的解。

 

程序24 用多利特尔或库朗直接分解法计算矩阵的逆矩阵。

输入：矩阵的阶数，矩阵的元素。

输出：的逆矩阵。

 

程序25用高斯-塞德尔法求解线性方程组。

输入：方程组的阶数，矩阵的元素和常向量的元素。

输出：方程组的解。

 

程序 随机形成元素值在20以内的三阶系数矩阵，使由它构造的雅可比迭代收敛，而高斯-塞德尔迭代不收敛。

输出：三阶系数矩阵。

 

程序 随机形成元素值在20以内的三阶系数矩阵，使由它构造的高斯-塞德尔迭代收敛，而雅可比迭代不收敛。

输出：三阶系数矩阵。

 

程序 随机形成元素值在-10到10以内的实系数矩阵，随机形成解向量的值，常向量的元素由算法得到；分别用列主元高斯消元法和高斯-塞德尔迭代法求解向性方程组，比较两种方法求解的效果和所用的CPU时间。

 

程序29 用雅可比方法计算实对称矩阵的全部特征值和特征向量。

输入：矩阵的阶数，矩阵的元素。

输出：矩阵的个特征值和特征向量。

 

程序30 用二阶龙格-库塔公式求解常微分方程组初值问题

（1），         （2）

输入：区间剖分点数n，区间端点a，b；定义函数

输出：

 

程序31 用四阶龙格-库塔公式(8.20)解初值问题计算公式

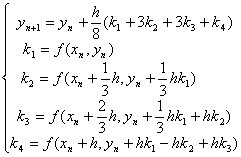
输入：区间剖分点数N，区间端点a，b；自定义函数

输出：，画出解曲线

 

程序32 用改进的欧拉公式求解常微分方程组初值问题

计算公式：

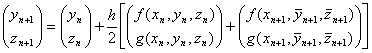
输入：区间剖分点数N，区间端点a，b；定义函数

输出：

 

程序33 用预估－校正公式解常微分方程组初值问题并与用改进的欧拉公式计算效果进行比较。

计算公式：

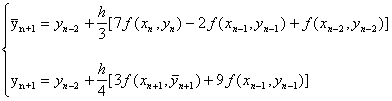
输入：区间剖分点数N，区间端点a，b；定义函数

输出：

 

l        上机语言

可用C语言、Fortran、Mathematica、Matlab、Maple等各种自选语言。

 

l        上机作业格式

*       题目

*       所用方法

*       实现算法

*       输入、输出说明

*       程序

*       运行结果

*       结果分析（选择项）