实验六 回转器的研究
一、实验目的
1． 了解回转器的基本特性及其运放实现。
2． 掌握回转器参数的测试方法，了解回转器的应用。
二、实验原理
回转器的概念是B.D.H.Tellegen于1948年提出的。六十年代由L.P.Huelsman及B.A.Sheei等人用运算放大器及晶体管电路实现。回转器是一种二端口器件，其电路符号如图6—1所示。它的电流与电压的关系为
I1=gU2
I2= — gU1
或写成
U1= －rI2
U2=rI1
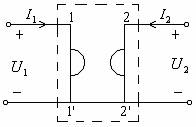
图6—1
式中g和r=
分别称为回转电导和回转电阻，简称回转常数。用矩阵形式可表示为
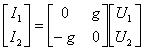
或
若在回转器2—2′端口接以负载阻抗ZL，则在1—1′端口看入的输入阻抗为
如果负载阻抗ZL在1—1′端口，则从2—2′端口看入的等效阻抗为
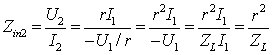
由上可见，回转器的一个端口的阻抗是另一端口的阻抗的倒数(乘上一定比例常数)，且与方向无关(即具有双向性质)。利用这种性质，回转器可以把一个电容元件“回转”成一个电感元件或反之。例如在2—2端口接入电容C，在正弦稳态条件下,即ZL=
，则在1－1′端口看入的等效阻抗为
式中，
为1—1′端口看入的等效电感。
同样，在1—1′端接电容Ｃ，在正弦稳态条件下，从2—2′看进去的输入阻抗Ｚin2为
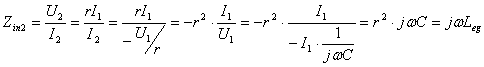式中Ｌeg＝r2C
可见回转器具有双向特性。
回转器具有的这种能方便地把电容“回转”成电感的性质在大规模集成电路生产中得到重要的应用。
回转器是一个无源元件。这可以证明如下，按回转器的定义公式，有
上式说明回转器既不发出功率又不消耗功率。
一般说来，线性定常无源双口网络满足互易定理，而回转器虽然也是属于线性定常无源网络，但并不满足互易定理。这一点可以简单论证如下。参照图6—1,如果在1—1′端口送入电流I1=1安，则在2—2′端口开路时，有I2=0,而U2=r伏。反之，在2—2′端口送入电流
安，在1—1′端口的开路电压
伏。可见
，即不满足互易定理。
回转器可以用多种方法来构成。现介绍一种基本构成方法。把回转器的导纳矩阵分解为
这样就可以用两个极性相反的电压控制电流源构成回转器，如图6—2所示。
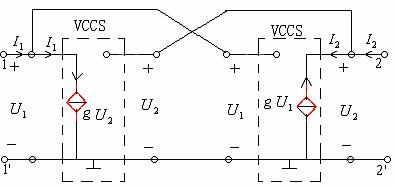
图6—2
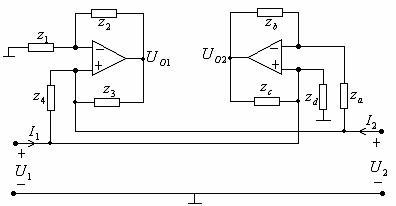
图6—3
本实验使用的回转器由两个运算放大器组成，如图6—3所示。假设：
1． 运算放大器是理想运算放大器，即：输入阻抗Zi→∞,流入两个输入端的电流为零，电压放大倍数A→∞，两个输入端的电压相等(虚短路)。
2． 回转器的输入幅度不超过允许值，以保证运算放大器在线性区工作。
根据以上假设，则图6—3中有：
容易推导图6—3二端口网络的电压、电流矩阵方程如下：
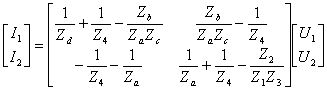
已知回转器的电压、电流矩阵方程为
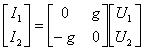
比较以上两个矩阵方程，应有
=0
=0
=g
= - g
现选定
Z1=Zd=R1=1KΩ Z2=Z3=Zc=R2=100Ω
Z4=Za=R3=2KΩ Zb=R4=300Ω
则回转电导为
或回转阻为
三、实验内容
1．测定回转电阻
(1) 接通电源，检查
15V电压，当电源接入正常时方可进行实验。
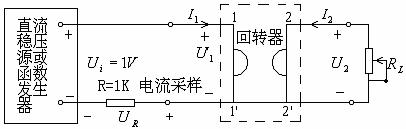
图6—4
(2)
按图6—4接线。调节RL为500Ω→∞范围内不同值时分别测量U1，U2及UR。将测量数据记入表1并计算出回转电阻ｒ。回转电阻可由下式求出：
。
表1
|
RL(Ω) |
500 |
1K |
2K |
4K |
7K |
12K |
20K |
32K |
50K |
∞ |
|
U1(V) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1=
UR/R(mA) |
|
|
|
|
|
|
|
|
|
|
|
U2(V)
|
|
|
|
|
|
|
|
|
|
|
|
I2=
-U2/RL(mA) |
|
|
|
|
|
|
|
|
|
|
|
r2=
U2/I1(Ω) |
|
|
|
|
|
|
|
|
|
|
|
r2=-U2/I2(Ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（3）注意事项
实验时既可采用直流稳压源提供的直流电压又可采用函数发生器提供的正弦交流电压。当采用直流电源时，输入电压和输入电流应分别不超过3V和3mA;当采用交流电源时，输入电压和输入电流的有效值应分别小于2V和2mA,频率可固定在200Hz。
2．验证回转器的线性性质r2=
U2/I1(Ω)
回转器在额定工作频率范围内是线性元件，这一点可以用图6—4的线
路加以验证。
(1) RL=2KΩ，改变稳压电源输出电压为不同值时分别测量U1及UR。将测量数据记入表2并计算出输入电阻
。
表2 RL=2KΩ
|
U1(V) |
|
|
|
|
|
|
|
|
3 |
2 |
1 |
-1 |
-2 |
-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) 固定RL=5KΩ，改变稳压电源输出电压为不同值时分别测量U1及UR。数据表格自行设计，并计算出输入电阻。
(3) 注意事项与实验内容1相同。
由实验数据验证： 
常数
3．验证非互易性
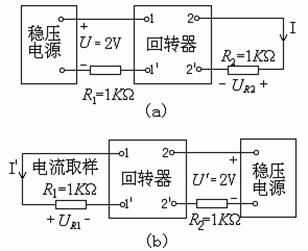
图6—5
(1) 按图6—5(a)接线。调节稳压电源输出电压使U=2V，用数字万用表测量UR2 。
(2) 按图6—5(b)接线。保持稳压电源输出电压使
V，用数字万用表测量UR1 (注意读数的正负性)。
(3) 数据表格自行设计。
4．用回转器和电容来模拟电感
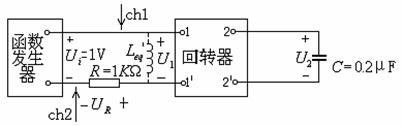
（ch2倒相） 图6—6
按图6—6接线。函数发生器选定正弦波输出，调节函数发生器输出电压使
=1V，在200Hz~1KHz范围内变化函数发生器频率（注意：频率变化时，负载变化，会有变化），用晶体管毫伏表测量在不同频率值时的Ui、U1及UR将数据记入表3，并计算出等效电感Leg。
表3
|
|
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
Ui(V) |
|
|
|
|
|
|
|
|
|
|
U1(V) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1= UR/R(mA) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5．回转器与两个电容器组成并联谐振电路
按图6—7接线。函数发生器选定正弦波输出，并保持发生器输出电压Ui=1V,在150HZ—800HZ范围内改变函数信号发生器的输出频率，用晶体管毫伏表测量在不同频率时的U1 记入表4。要仔细找出U1最大时的信号源频率(即谐振频率)并与理论计算的频率进行比较。
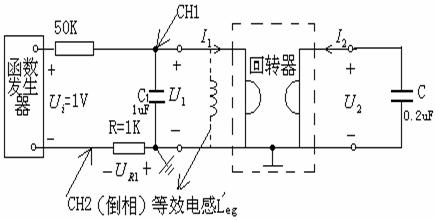图6—7
表4 =1V
|
f(HZ) |
150 |
|
|
|
|
|
|
800 |
|
U1(V) |
|
|
|
|
|
|
|
|
理论计算的谐振频率为
式中 Leg=r2C(H)
。
四、思考题
1. 总结回转器的性质、特点和应用。从你的实验数据能否证明回转器的无源性？
2. 测量回转电导(电阻)时，如果使用正弦信号和示波器，如何测出回转电阻，画出实验线路图。
3. 并联谐振时，为何要串联50KΩ电阻(甚至更大)？1KΩ电阻起何作用？
五、实验报告要求
1．完成以上实验内容所规定的计算，进行必要的分析比较。
2．回答思考题。
六、实验设备
1．
DJB—3型电路分析实验箱和回转器实验板 1套
2．
DF1731SB2A型或DF1733型直流稳压稳流源 1台
3．
DF1641D型或EE1641D型函数发生器1台
4．
UT-56数字万用表1块
5．
双踪示波器 1 台
6．
可变电阻箱 2个
7．
可变电容箱 2个
8．
晶体管毫伏表1 台