实验十四 非线性电阻电路的研究
一、实验目的
1. 了解非线性电阻电路的一般分析方法。
2. 掌握非线性电阻元件的组合特性。
3. 掌握非线性电阻元件的应用。
二、实验原理
由线性元件构成的电路称为线性电路。若电路中含有非线性元件则称为非线性电路。根据线性电路建立的电路方程都是线性方程,求解比较方便。但对于非线性电路的分析求解就复杂得多。我们知道非线性元件的电特性往往是以曲线的形式给出的,有时也可以用解析式近似描述,但因它们都是非线性函数,所以对电路建立的电路方程也是非线性的。通常对非线性方程是无法用解析的方法求出最终结果的。这就是分析非线性电路要比分析线性电路复杂得多的原因。分析非线性电路通常采用的有三种方法:图解法,分段线性化和数值解法。
1.非线性电阻元件的联接
对于线性电阻元件的简单联接,通过简单的代数运算就可以求出它们的等效电阻。但是对于非线性电阻简单联接的处理方法就不那么方便,需要用图解法求解。
设已知各非线性电阻(例如二极管)的伏安特性曲线如图14—1中(b)所示,两个二极管串联如图14—1中(a)所示。现在我们要确定它们串联后的特性曲线,即串联等效电阻的特性曲线。
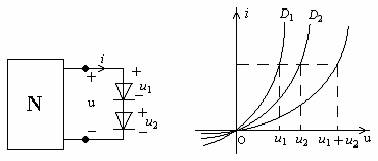
(a) (b)
图14—1
在图14—1(a)中,根据基尔霍夫定律有
![]() (14—1)
(14—1)
因此,只要对每一个指定的电流i,把它在![]() 和
和![]() 特性曲线上对应的电压值
特性曲线上对应的电压值![]() 和
和![]() 相加,就可以得到串联后的特性曲线,如图14—1(b)所示。根据等效的定义这条曲线就是串联等效电阻的特性曲线。可见,此特性曲线仍是非线性的。
相加,就可以得到串联后的特性曲线,如图14—1(b)所示。根据等效的定义这条曲线就是串联等效电阻的特性曲线。可见,此特性曲线仍是非线性的。
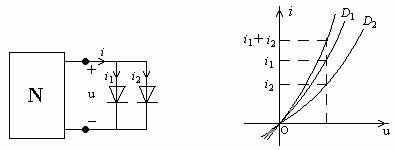
(a) (b)
图14—2
对非线性电阻的并联电路,也可作类似的处理。设电路如图14—2(a)所示,两非线性电阻的伏安特性曲线如图14—2(b)中的![]() 和
和![]() 所示,由KCL及KVL知:
所示,由KCL及KVL知:
![]() (14—2)
(14—2)
所以只对第一个指定的电压u,把它在![]() 和
和![]() 特性曲线上对应的电流
特性曲线上对应的电流![]() 和
和![]() 相加,便可得如图14—2(b)所示并联后的特性曲线。
相加,便可得如图14—2(b)所示并联后的特性曲线。
混联电路也可作类似的处理。如果混联电路由两个非线性电阻并联后再与另一非线性电阻串联组成,可先求出并联部分的特性曲线,再按串联电路处理,最后求得混联等效电阻的特性曲线。
2.非线性电阻电路的分析
电路分析的最终目的是要求出电路中各支路电压和电流。电路不管是线性的还是非线性的,求解的基本依据都是基尔霍夫电流、电压定律和元件的伏安特性,只是对于非线性电阻电路中非线性电阻元件的特性曲线是非线性的,对电路写出的电路方程是非线性方程。因此,在一般情况下无法用单纯的解析法完成求解任务。下面结合电路图14—3来说明非线性电阻的分析。
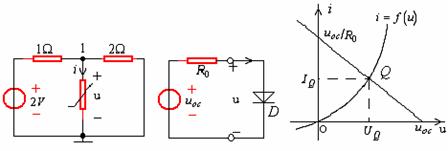
(a) (b) (c)
图14—3
(1)计算法。在图14—3(a)中,若非线性电阻的VAR为:![]() ,试求电流I。
,试求电流I。
解:一般非线性电阻的符号如图14—3(a)中所示,在节点(1)处由KCL得:
![]()
将![]() 代入上式得:
代入上式得:
![]()
解得:![]()
因此,有两组解答:
![]()
(2)图解法。在图14—3(b)中,是含有一个非线性元件的电阻电路。我们可以把原电路看成是由两个单口网络组成的,一个单口为电路的线性部分,另一则为非线性部分。线性部分可用戴维南等效电路或诺顿等效电路表示。
线性单口部分用戴维南等效表示后如图14—3(b)所示。给定非线性电阻的VAR后,就可和线性部分的VAR联立,求得端口电压u和电流i,亦即非线性元件两端的电压和流过的电流。设非线性电阻的VAR为如图14—3(c)所示,经常是用u-i平面上的曲线表示。
![]() (14—3)
(14—3)
线性部分的VAR为
![]() (14—4)
(14—4)
我们用图解法求解u和i。为此,我们在表明![]() 的同一u-i平面上,绘出(14—4)式的VAR曲线。在u-i平面上这是一条斜率为
的同一u-i平面上,绘出(14—4)式的VAR曲线。在u-i平面上这是一条斜率为![]() 的直线,纵轴截距为
的直线,纵轴截距为![]() ,如图14—3(c)所示,两曲线的交点便是所求的解答。解答点
,如图14—3(c)所示,两曲线的交点便是所求的解答。解答点![]() 称作工作点,图中的直线称为“负载线”。求得端口电压
称作工作点,图中的直线称为“负载线”。求得端口电压![]() 和电流
和电流![]() 后,就可用置换定理求得线性单口网络内部的电压和电流。上述方法通常称为“负载线法”。
后,就可用置换定理求得线性单口网络内部的电压和电流。上述方法通常称为“负载线法”。
(3)非线性电阻电路的分段线性分析。分段线性化分析法就是把原来用以表示非线性电阻元件的伏安特性曲线用折线近似表示。这样,折线的每一直线段就可以用直线函数确切描述。从而可表示成代数方程的形式。一旦每一直线段都可用代数方程表达,就可逐段的对电路进行定量分析。
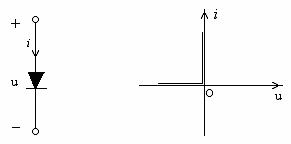
图14—4
根据分段线性化的方法,我们可以定义一个理想二极管的模型。如果一个二端的非线性电阻在u-i平面上的特性曲线由负u轴和正的i轴这样两条直线段组成,则称为理想二极管。理想二极管的符号及其特性曲线如图14—4所示,理想二极管的特性可解析地表示为:
![]() 对所有的
对所有的![]()
![]() 对所有的
对所有的![]()
也可以说,理想二极管相当于一个理想开关,导通时相当于开关闭合,起着短路作用,电阻为零,截止时相当于开关断开,起着开路作用,电阻为无穷大。特性曲线的原点称为“转折点”。
分析含理想二极管的电路时,关键在于确定二极管是正向偏置(导通)还是反向偏置(截止)。如属前一情况,则二极管以短路线代替,如属后一情况,则二极管以开路代替,代替后都可得到一个线性电阻电路,易于求得结果。当电路中只含一个理想二极管时,可用戴维南定理解题而不需要用图解法。
如果电路中含有多个理想二极管,可用假定状态法分析电路。设含三个理想二极管的电路如图14—5所示,要求计算![]() 。分析这类电路时应找出在公共输出端的各二极管中正向电压最大的一个,这一个二极管优先导通。据此作出假定后再去分析各二极管的状态是否合乎假定。
。分析这类电路时应找出在公共输出端的各二极管中正向电压最大的一个,这一个二极管优先导通。据此作出假定后再去分析各二极管的状态是否合乎假定。
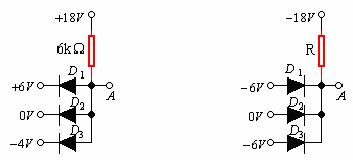
图14—5
(4)非线性电阻电路的小信号分析。
在电子电路分析中,经常遇到激励信号变化幅度很小的情况,这时可以围绕工作点建立一个局部的线性模型。对小信号来说,我们可以根据这种模型运用线性电路的分析方法进行研究,这就是非线性电路的小信号分析。
前面图14—3中,我们介绍了“工作点”的概念。在此基础上来讨论非线性电阻小信号分析。设在图14—3(b)中除直流电压源![]() 外,再接入一个时变电压源
外,再接入一个时变电压源![]() ,如图14—6(a)并假定对所有时间t有
,如图14—6(a)并假定对所有时间t有![]() ,即该时变电压的绝对值在所有时间均远小于直流电源电压。在实际应用中,时变电源称为信号,而直流电源则称为偏置。现在要求解出非线性电阻的端电压u
,即该时变电压的绝对值在所有时间均远小于直流电源电压。在实际应用中,时变电源称为信号,而直流电源则称为偏置。现在要求解出非线性电阻的端电压u![]() 和流过它的电流
和流过它的电流![]() 。在这种情况下,描述电路的约束方程应为:
。在这种情况下,描述电路的约束方程应为:
![]() (14—5)
(14—5)
![]() (14—6)
(14—6)
式中,![]() 表示非线性电阻的伏安特性。
表示非线性电阻的伏安特性。
在每时刻t,满足(14—5)式的所有点![]() 的轨迹是图14—6(b)中u-i平面上的一条平行于原负载线的直线。如果
的轨迹是图14—6(b)中u-i平面上的一条平行于原负载线的直线。如果![]() >0,则该直线位于原负载线的上方,如果
>0,则该直线位于原负载线的上方,如果![]() ,则位于下方。满足方程(14—6)的所有点
,则位于下方。满足方程(14—6)的所有点![]() 的轨迹,仍然是原不随时间变化的非线性电阻的伏安特性曲线。所以,凡同时位于直线上的任意点
的轨迹,仍然是原不随时间变化的非线性电阻的伏安特性曲线。所以,凡同时位于直线上的任意点![]() ,必须满足方程(14—5)和(14—6),这就是说它们的交点就是所求的解,可以用图解法作出解答。
,必须满足方程(14—5)和(14—6),这就是说它们的交点就是所求的解,可以用图解法作出解答。
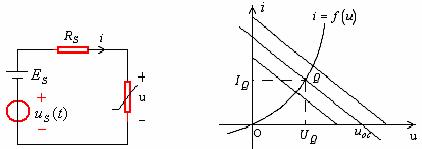
(a) (b)
图14—6
由于我们假定![]() 足够小,则解答
足够小,则解答![]() 必位于工作点
必位于工作点![]() 近旁,即
近旁,即
![]() (14—7)
(14—7)
![]() (14—8)
(14—8)
式中,![]() 和
和![]() 可看成是直流解
可看成是直流解![]() 的扰动,这种扰动是由小信号电压
的扰动,这种扰动是由小信号电压![]() 引起的。
引起的。
将式(14—7)和(14—8)代入非线性电阻方程式(14—6)有
![]()
因![]() 足够小,所以可用台劳级数将上式的右方在
足够小,所以可用台劳级数将上式的右方在![]() 点展开,并取其前两项,得
点展开,并取其前两项,得
![]() (14—9)
(14—9)
根据式![]() ,可得到关于增量电压
,可得到关于增量电压![]() 和增量电流
和增量电流![]() 的方程,即
的方程,即
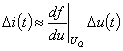
式中,![]() 是非线性电阻特性曲线在工作点
是非线性电阻特性曲线在工作点![]() 处的斜率,令
处的斜率,令
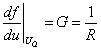
G称为非线性电阻在工作点处的增量电导或动态电导,图14—6(b)的伏安特性曲线在工作点Q处的斜率。对时变电压![]() 和增量电流
和增量电流![]() 来说,G为一常数,相当于一线性电阻,于是有:
来说,G为一常数,相当于一线性电阻,于是有:
![]() (14—10)
(14—10)
![]() (14—11)
(14—11)
把上述结果,连公式(14—7)和(14—8)代入(14—5)式得
![]()
我们可以得到![]() 和
和![]() 的线性方程组,联立求解,而得
的线性方程组,联立求解,而得
![]()
![]()
将此结果与工作点电压和电流结合起来就是所求的解答
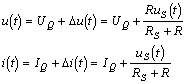
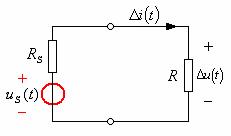
图14—7
根据式(14—10)和(14—11)画出非线性电阻对工作点Q而言的小信号的线性电路模型,如图14—7所示。应当注意,工作点不同,在工作点处的斜率就不同,小信号线性等效电路的电路参数R的数值也就不同。
三、实验内容
1.二极管VAR曲线的测量
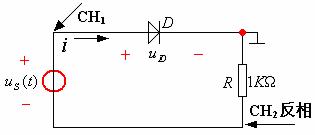
图14—8
按图14—8接线,![]() ,正弦信号
,正弦信号![]() ,图中
,图中![]() 为限流电阻(负载),如果
为限流电阻(负载),如果![]() ,则要烧坏二极管,用李沙育图形画出VAR曲线,并标出最大正向电压,正向电流,最大反向电压,门限电压
,则要烧坏二极管,用李沙育图形画出VAR曲线,并标出最大正向电压,正向电流,最大反向电压,门限电压![]() 。
。
2.稳压管VAR曲线的测量
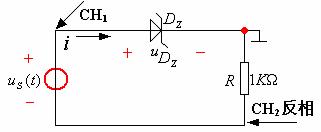
图14—9
按图14—9接线,![]() 正弦信号,
正弦信号,![]() , (因为稳压管主要用反向特性,稳压电压
, (因为稳压管主要用反向特性,稳压电压![]() 根据管子不同,有的为
根据管子不同,有的为![]() ,有的为
,有的为![]() 等)。用李沙育图形画出VAR曲线,并标出最大正向电压,正向电流,正向门限电压
等)。用李沙育图形画出VAR曲线,并标出最大正向电压,正向电流,正向门限电压![]() ,稳压电压
,稳压电压![]() ,最小稳定电流。
,最小稳定电流。
3.逻辑电路(门电路)
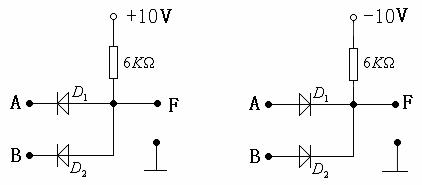
(a) (b)
图14—10
图14—10(a)为与门电路,根据输入A、B的电位不同,(用![]() 表示低电位,如
表示低电位,如![]() ,用
,用![]() 表示高电位,如
表示高电位,如![]() ),有
),有![]() ,用假定状态法,分析
,用假定状态法,分析![]() ,
,![]() 的导通、截止情况,并完成
的导通、截止情况,并完成![]() 的测量:
的测量:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
图14—10(b)为或门电路,根据输入A、B的电位不同,有![]() ,用假定状态法,分析
,用假定状态法,分析![]() ,
,![]() 的导通、截止情况,并完成
的导通、截止情况,并完成![]() 的测量:
的测量:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.组合VAR曲线的测量
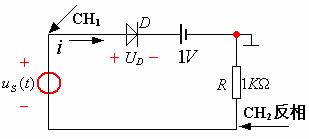
图14—11
按图14—11接线,![]() 正弦信号
正弦信号![]() ,用李沙育图形画出VAR曲线,在电子线路中称为钳位电路。
,用李沙育图形画出VAR曲线,在电子线路中称为钳位电路。
5. 转移特性曲线的测量
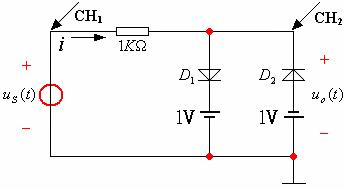
图14—12
按图14—12接线,![]() 正弦信号
正弦信号![]() ,用示波器画出
,用示波器画出![]() 的转移特性曲线。在电子线路中称为双向限幅电路。
的转移特性曲线。在电子线路中称为双向限幅电路。
6.简单非线性电阻电路的小信号分析法
(1) 直流工作点
① 负载线法
按图14-8(a)接线,测出其二极管的伏安特性曲线并绘出。在以上所作的伏安特性曲线上作出一条斜率为![]() 的直线,纵轴截距为
的直线,纵轴截距为![]() 。两曲线的交点便是所求的解答。解答点
。两曲线的交点便是所求的解答。解答点![]() 称为非线性元件的“工作点”,而直线AB称为“负载线”,求得的端口电压
称为非线性元件的“工作点”,而直线AB称为“负载线”,求得的端口电压![]() 和电流
和电流![]() 后,就可用置换定理进一步求其他电压和电流。
后,就可用置换定理进一步求其他电压和电流。
②
图14-13(a)所示为实验线路图;![]() 伏,
伏,
设![]() ;作出稳压二极管伏安特性曲线
;作出稳压二极管伏安特性曲线![]() 。
。
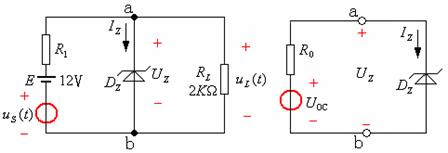
(a) (b)
图14—13
图14—13(a)所示的实验线路,从ab两点看进去的戴维南等效电路如图14—13(b)所示。UOC为ab支路所接的二极管断开时的开路电压;R0为等效电阻。直线方程![]() ,在稳压管特性曲线上作出直线AB交特性曲线于Q点。Q点坐标为直流工作点Q(UQ,IQ)。实验中,按图14—13接线,直流电源
,在稳压管特性曲线上作出直线AB交特性曲线于Q点。Q点坐标为直流工作点Q(UQ,IQ)。实验中,按图14—13接线,直流电源![]() ,
,![]() (短路) ,调R1,使
(短路) ,调R1,使![]() 用万用表测出UZ即为UQ。
用万用表测出UZ即为UQ。
(2)求动态电阻![]()
按图14—13(a)接线,直流电源![]() ,
,![]() (短路) ,用万用表DCV档测出
(短路) ,用万用表DCV档测出![]() 。
。
加上正弦信号![]() 伏,其有效值用晶体管毫伏表来测量。再用毫伏表测出
伏,其有效值用晶体管毫伏表来测量。再用毫伏表测出![]() 上的电压
上的电压![]() ,求出流过
,求出流过![]() 的电流
的电流![]() ,用毫伏表测出
,用毫伏表测出![]() 上电压的
上电压的![]() ,求出流过
,求出流过![]() 的电流
的电流![]() ,流过稳压管的电流为
,流过稳压管的电流为![]() ,则
,则![]() 。稳压管显然可以用一个理想电压源
。稳压管显然可以用一个理想电压源![]() 和一个电阻
和一个电阻![]() 等效,如图14—14所示。
等效,如图14—14所示。
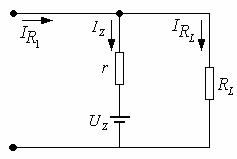
图14—14
四、思考题
1. 小结对非线性电路的分析方法?
2. 理想二极管的特性是什么?
3. 据你所知,非线性元件有哪些应用?
4. 根据实验内容6,说明稳压管的稳压原理?
5. 利用二极管的正向特性,能否起稳压作用?
6. 理想电压源、理想电流源是压控还是流控?(在![]() 平面上)
平面上)
五、实验仪器
1. 函数信号发生器
2. 双踪示波器
3. 晶体管毫表
4. 数字万用表
5. 二极管、稳压管
6. 可变电阻箱