实验十一 无源滤波器的研究
一、实验目的
1.掌握测定R、C无源滤波器的幅频特性的方法。
2.了解由R、C构成的一些简单的二阶无源滤波电路及其特性。
3.通过理论分析和实验测试加深对无源滤波器的认识。
二、实验原理
滤波器是一种选择装置,它对输入信号进行加工和处理,从中选出某些特定的信号作为输出。电滤波器的任务是对输入信号进行选频加权传输。
电滤波器是Campbell和wagner在第一次世界大战期间各自独立发明的,当时直接应用于长途载波电话等通信系统。电滤波器主要由无源元件R、L、C构成,称为无源滤波器。
滤波器的输出与输入关系通常用电压转移函数H(S)来描述,电压转移函数又称为电压增益函数,它的定义如下
![]()
式中UO(S)、Ui(S)分别为输出、输入电压的拉氏变换。在正弦稳态情况下,S=jω,电压转移函数可写成
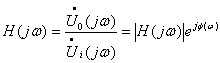
式中![]() 表示输出与输入的幅值比,称为幅值函数或增益函数,它与频率的关系称为幅频特性;F(ω)表示输出与输入的相位差,称为相位函数,它与频率的关系称为相频特性。幅频特性与相频特性统称滤波器的频率响应。滤波器的幅频特性很容易用实验方法测定。
表示输出与输入的幅值比,称为幅值函数或增益函数,它与频率的关系称为幅频特性;F(ω)表示输出与输入的相位差,称为相位函数,它与频率的关系称为相频特性。幅频特性与相频特性统称滤波器的频率响应。滤波器的幅频特性很容易用实验方法测定。
本实验仅研究一些基本的二阶滤波电路。滤波器按幅频特性的不同,可分为低通、高通、带通和带阻和全通滤波电路等几种,图附录1—1给出了低通、高通、带通和带阻滤波电的典型幅频特性。
低通滤波电路,其幅频响应如图附录1—1(a)所示,图中|H(jωC)|为增益的幅值,K为增益常数。由图可知,它的功能是通过从零到某一截止频率ωC的低频信号,而对大于ωC的所有频率则衰减,因此其带宽B=ωC。
高通滤波电路,其幅频响应如图附录1—1(b)所示。由图可以看到,在0<ω<ωC范围内的频率为阻带,高于ωC的频率为通带。
带通滤波电路,其幅频响应如图附录1—1(c)所示。图中ωCl为下截止频率,ωCh为上截止频率,ω0为中心频率。由图可知,它有两个阻带:0<ω<ωCl和ω>ωCh,因此带宽B=ωCh-ωCl。
带阻滤波电路,其幅频响应如图附录1—1(d)所示。由图可知,它有两个通带:0<ω<ωCl及ω>ωCh和一个阻带ωCl<ω<ωCh。因此它的功能是衰减ωCl到ωCh间的信号。通带ω>ωCh也是有限的。
带阻滤波电路阻带中点所在的频率ωZ叫零点频率。
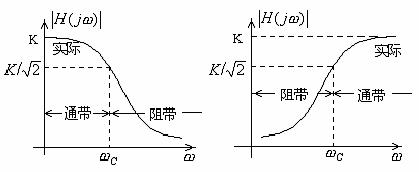
(a)低通滤波电路 (b)高通滤波电路
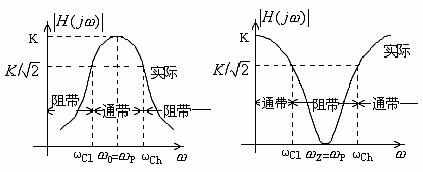
(c)带通滤波电路 (d)带阻滤波电路
图附录1—1 各种滤波电路的幅频响应
二阶基本节低通、高通、带通和带阻滤波器的电压转移函数分别为
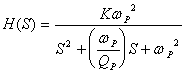 低通
低通
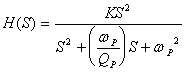 高通
高通
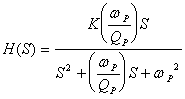 带通
带通
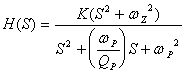 带阻
带阻
式中K、ωp、ωz和Qp分别称为增益常数、极点频率、零点频率和极偶品质因数。正弦稳态时的电压转移函数可分别写成
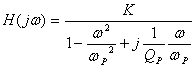 低通
低通
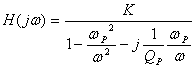 高通
高通
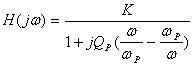 带通
带通
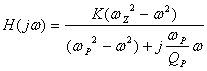 带阻
带阻
三、实验内容
1.二阶无源低通滤波器
(1)二阶无源RC低通滤波器的幅频特性
图附录1—2所示电路为二阶无源RC低通滤波器基本节,采用复频域分析,可以得其电压转移函数为:
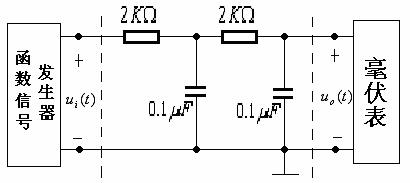
图附录1—2
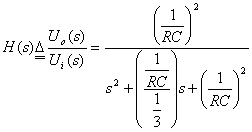
根据二阶基本节低通滤波器电压转移函数的典型表达式:
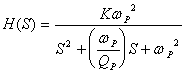
可得增益常数K=1,极点频率![]() 和极偶品质因数
和极偶品质因数![]() 。
。
正弦稳态时,电压转移函数可写成:
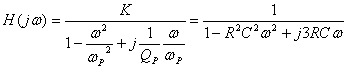
幅值函数为:
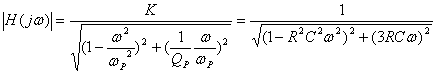
由上式可知:
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
可见随着频率升高幅值函数值减小,该电路具有使低频信号通过的特性,故称为低通滤波器。
(2)实验步骤与注意事项
按图附录1—2接线。函数信号发生器选定为正弦波输出,固定输出信号幅度为![]() ,改变
,改变![]() (零频率可以用
(零频率可以用![]() ,或
,或![]() 近似)从40Hz~3KHz范围内不同值时,用毫伏表测量
近似)从40Hz~3KHz范围内不同值时,用毫伏表测量![]() 。要求找出极点频率
。要求找出极点频率![]() 和截止频率
和截止频率![]() 的位量,其余各点频率由学生自行决定,数据填入表1中。画出此滤波器的幅频特性曲线,并进行误差分析。
的位量,其余各点频率由学生自行决定,数据填入表1中。画出此滤波器的幅频特性曲线,并进行误差分析。
注:当![]() 时,对应的频率称为
时,对应的频率称为![]() (
(![]() );截止频率
);截止频率![]() (
(![]() )是幅值函数自
)是幅值函数自![]() 下降3db,即
下降3db,即![]() 时,所对应的频率。
时,所对应的频率。
每次改变频率时都应该注意函数发生器的输出幅度为Uip-p=1V。我们可以用示波器来监视函数信号发生器的输出幅度。
![]()
表1
|
|
40 |
|
|
|
|
|
|
|
|
3K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2.二阶高通滤波器
(1) 二阶无源RC高通滤波器的幅频特性
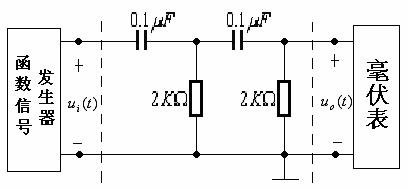
图附录1—3
图附录1—3所示电路为二阶无源RC高通滤波器基本节,采用复频域分析,可以得其电压转移函数为:
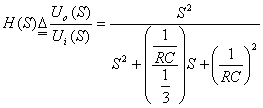
根据二阶基本节高通滤波器电压转移函数的典型表达式:
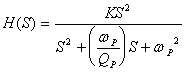
可得增益常数K=1,极点频率![]() ,极偶品质因数
,极偶品质因数![]() 。
。
正弦稳态时,电压转移函数可写成:
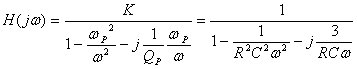
幅值函数为:
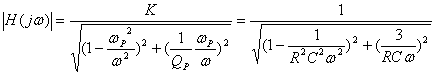
由上式可知:
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
可见随着频率增加幅值函数增大,该电路具有使高频信号通过的特性,故称为高频滤波器。
(2) 实验步骤与注意事项
按图附录1—3接线。除正弦信号频率范围取100Hz~10KHz外,操作步骤与注意事项和二阶无源RC低通滤波器相同。要求找出![]() 和
和![]() ,数据填入表2中。画出此滤波器的幅频特性曲线,并进行误差分析。
,数据填入表2中。画出此滤波器的幅频特性曲线,并进行误差分析。
![]()
表2
|
|
100 |
|
|
|
|
|
|
|
|
10K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3.二阶带通滤波器
(1)二阶无源RC带通滤波器的幅频特性
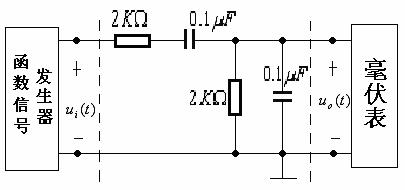
图附录1—4
图附录1—4所示电路为二阶无源RC带通滤波器基本节,采用复频域分析,可以得其电压转移函数为:
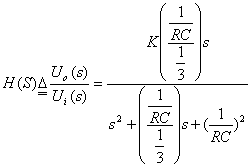
根据二阶基本节带通滤波器电压转移函数的典型表达式:
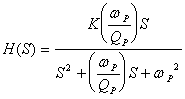
可得增益常数![]() ,极点频率
,极点频率![]() ,极偶品质因数
,极偶品质因数![]() 。
。
正弦稳态时,电压转移函数可写成:
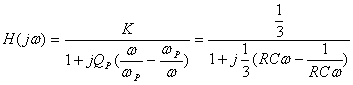
幅值函数为:

当![]() 时,
时,![]() 称为带通滤波器的中心频率,即
称为带通滤波器的中心频率,即
![]()
截止频率![]() 是幅值函数自
是幅值函数自![]() 下降3db(即
下降3db(即![]() )时所对应的频率。由|H(jω)|的表达式可得
)时所对应的频率。由|H(jω)|的表达式可得
![]()
对上式求解得
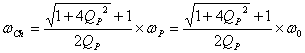
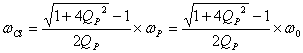
![]() ,
,![]() 分别称为上截止频率和下截止频率。
分别称为上截止频率和下截止频率。
通频带宽度B为
![]()
品质因数Q为
![]()
可见二阶带通滤波器的品质因数Q等于极偶品质因数Qp。Q是衡量带通滤波器的频率选择能力的一个重要指标。
由|H(jω)|的表达式可知:
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
信号频率偏离中心频率![]() 越远,幅值函数衰减越大。由于品质因数
越远,幅值函数衰减越大。由于品质因数
![]()
说明无源低通滤波器的品质因数太低,通频带宽度![]() 很宽,故滤波器的选择性差。
很宽,故滤波器的选择性差。
(2)实验步骤与注意事项
按图附录1—4接线。除正弦信号频率范围取100Hz~8KHz外,操作步骤与注意事项和二阶无源RC低通滤波器相同。要求找出![]() 、
、![]() 和
和![]() 的位量,数据填入表3中。画出此滤波器的幅频特性曲线,并进行误差分析。
的位量,数据填入表3中。画出此滤波器的幅频特性曲线,并进行误差分析。
![]()
表3
|
|
100 |
|
|
|
|
|
|
|
|
8K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
四、思考题
1. 从滤波器的一些数学表达中,你如何理解滤波的概念?
2.
在频域分析中,研究![]() 和
和![]() 有何意义?
有何意义?
3. 从低通、高通、带通滤波器的幅频特性说明中,你认为全通滤波的幅频特性应当如何?
五、实验设备
1. 函数信号发生器
2. 晶体管毫伏表
3. 双踪示波器
4. 可变电容箱
5. 可变电阻箱