前言

本学期塞曼效应实验是在已知Hg5461埃跃迁型条件下求荷质比。这里反其道行之，在已知荷质比条件下，并假设Hg的两个价电子为LS耦合，来确定Hg5461埃的跃迁类型：

 

实验现象及结果

其步骤与原实验相同，不再复述.观察实验现象如下:用滤波器区分ΔM=0和ΔM=±1的跃迁.ΔM=0的跃迁可观察到三组干渉环，中间一组与零场相同，内外两侧与零场间距相等.ΔM=±1跃迁在外场B不太强的情况下，即没有重叠时，可观察到六组干涉环，也分居零场干涉环两侧，其间距绝对值有三个不同值。由F-P干涉仪光学性质关系式(详见第三册实验书之塞曼效应)可得：

其中D_n’是零场第n组环直径， D_n是上述环外场中位移后的直径，d为干涉仪隔圈间距。

测量结果如下：

d=4.9999±0.0002mm，D_n²-D_n-1²的平均值约为12.78cm²，外磁场强度B约为1000mT，ΔM=0对应的D_n’ ²-D_n²约为3.97cm²， ΔM=±1对应的D_n’ ²-D_n²约为2.54cm²，(仅取一组位移干涉环)

将以上数据代入(1)式，得出结果:

ΔM=0时ΔMg=0.45±0.09        (2)

ΔM=±1时ΔMg=1.11±0.21      (3)

n        讨论分析：

 

由假定可知,LS耦合的选择定则为：

ΔS=0       (4)

ΔL=0，±1     (5)

ΔL=0，±1(J=0®J=0除外)      (6)

ΔJ=0，±1(M=0®M=0除外)   (7)

还有关系式：

J=L+S，L+S-1，¼，|L-S|        (9)

M=J，J-1，¼，-J+1，-J          (10)

=      由(1)式Δ(Mg)=M_上g_上- M_下g_下，又由(2)得

ΔM=0时可令M_上=M_下=M 则

Δ(Mg)= M(g_上-g_下)¹0则

g_上-g_下¹0

\g_上¹g_下             (11)

=      由(7)式ΔJ=0，±1假设ΔJ=0则由选择定则(5)可知：ΔM=0中M_上=0到M_下=0的跃迁被禁止，也即Δ(Mg)=0的跃迁被禁止，即外场中没有零场时的干涉环。这与现象矛盾，所以假设错误，则ΔJ¹0所以有

ΔJ= ±1        (12)

=      由(12) ΔJ= ±1可设J_上和J_下为J₁和J₂，并令J₂= J₁+1则由(10)得

由(4)及现象可知ΔM=0对应跃迁为以上连线，共三条，所以

J₁=1，J₂=2   (13)

=      因为Hg仅有两个价电子，所有各能级上总自旋S取0、1两值之一。再由(7)

J=L+S，L+S-1，¼，|L-S|

确定L值，下图给出(13) J₁=1，J₂=2时各原子态及朗德因子：

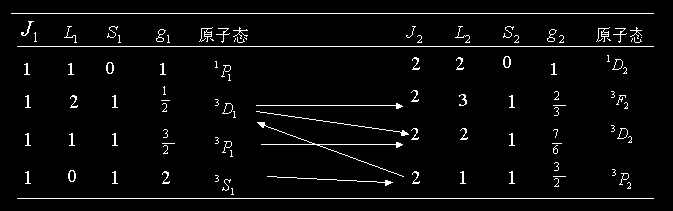
由选择定则(4)(5)：ΔS=0，ΔL=0，±1及(11) g_上¹g_下得出Hg5461埃可能的跃迁类型,又因为LS耦合满足洪特规则，即可确定上下能级，决定箭头方向，出射方为上能级，所指方为下能级。

=      现在可列出可以配对的朗德因子及相应的Δ(Mg)值,例如

其余作法类似,不再累述,列成下表：

结论：

由实验结果(2)(3)：ΔM=0时Δ(Mg)存在值0.45+0.09»1/2

ΔM=±1时Δ(Mg)存在值1.11+0.21»3/2

属于上表中³S₁®³P₂型跃迁产生,所以确定Hg5461埃谱线跃迁类型为³S₁®³P₂

n        小结

在原子数不太大，价电子数较少的情况下，即LS耦合时，可用这种方法来确定跃迁类型。