实验内容

对CCl4偏振特性进行了测量，并通过和理论计算结果的比较，了解分子结构和振动的对称性与拉曼光谱的偏振特性之间的关系。

实验原理部分

1、拉曼散射的原理

拉曼散射是光和物质相互作用引起的，光子和散射物质分子碰撞过程中，散射物质可能会从入射光子吸收部分能量或把自身部分能量加到入射光子上去，因此发射的散射光中既有与入射光频率相同的谱线，也有与入射光频率不同的谱线，前者称为瑞利线，后者称为拉曼线。在拉曼线中，又把频率小于入射光频率的谱线称为斯托克斯线，而把频率大于入射光频率的谱线称为反斯托克斯线。

对此可以从半经典的量子理论进行解释：

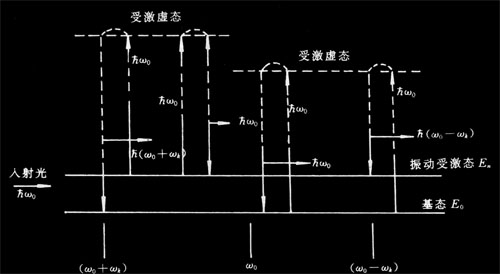
设散射物分子原来处于某一状态（基态或是激发态），当受到入射光照射时，电子被激发跃迁到一个中间态（量子理论中称为虚能态），虚能态上的电子立即跃迁到下能级而发光，即为散射光，如图所示，有三种情况，分别对应反斯托克斯线，瑞利线和斯托克斯线。

拉曼光谱有如下基本特点：

a.在以频率（波数）为变量的拉曼光谱图上，斯托克斯线和反斯托克斯线对称地分布在瑞利散射线两侧；

b. 对同一样品，虽然激发光频率不同，拉曼散射谱线的频率也不同，但同一拉曼谱线的频率位移 与入射光的频率无关，只和样品本身的结构有关；

c.一般情况下，斯托克斯线比反斯托克斯线的强度大。这是由于玻尔兹曼分布下，处于振动基态上的粒子数远大于处于振动激发态上的粒子数。

同时，拉曼效应也可以用经典电磁理论来解释，同样可以说明偏振现象和解释散射频率。比如分子在激发光的交变场下发生感生极化，成为电偶极子。电偶极子随激发场交变振荡而成为辐射体，与入射光同步发射，则成为瑞利散射；若受自身振动和转动频率调制，则会改变其极化率，散射光中出现 的频率。对于偏振，由于感生偶极距和外场振动方向一致，辐射的偏振特性也就可由偶极子辐射得知。下面就是用经典的方法来处理拉曼光谱的偏振特性，结果和用量子理论处理是一致的。

2、拉曼光谱的退偏度

当电磁辐射与一系统相互作用时，偏振态常发生变化，这种现象称为退偏。在拉曼散射中，这种退偏度和分子的对称性是密切相关的。

下面一步步地进行说明：

由于偏振状态取决于入射光的偏振状态、散射系统的取向和观察方向，所以先要定义一个参考平面，取入射光传播方向和观测方向组成的平面，称为散射平面。

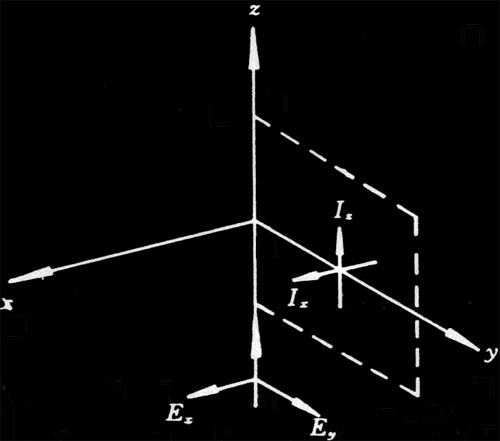
当入射光为平面偏振光，且偏振方向垂直于散射平面，而观测方向在散射平面内与入射光传播方向成 角时，定义退偏度为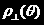；当入射光偏振方向平行于散射平面时，定义退偏度为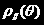，具体形式为：

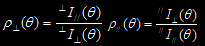
光强I左上标表示入射光的电矢量与散射平面的关系,I的右下标表示散射光的电矢量与散射平面的关系。

当入射光为自然光时，有

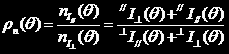
例如，入射光沿z轴入射，沿x轴方向偏振时，散射平面为y-z平面，沿y轴观察时，其退偏度为

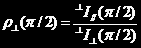
由理论计算可知，对于入射光为线偏光的情况，有

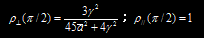
对于自然光，则有

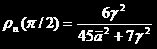
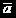是平均极化率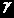，是各项异性率（在后面有详细的说明），这些关系是连接偏振特性和分子结构的桥梁。（注：理论计算部分参考自《拉曼光谱学》，D.A.朗著，这里略去。）

3、CCl4退偏度的理论计算

粗略地看，按波尔兹曼分布律，处于激发态Ei的分子数Ni与处于正常态E0分子数N0之比是：CCl4分子为四面体结构，一个碳原子在中心，四个氯原子在四面体的四个顶点，共有9种简正振动，除去简并，可归成四种:

a. 4个Cl原子沿各自与c 的连线同时向外或向内运动(呼吸式)。

b. 4个Cl沿垂直于各自与c的连线的方向运动并保持重心不变，两重简并。

c. C原子平行于正方形的一边运动，4个Cl原子同时平行于该边反向运动。分子重心保持不变，三重简并。

d. 2个Cl原子沿立方体一面的对角线做伸缩运动，另两个在对面做位相相反的运动，也是三重简并。

以上四种振动方式对应于拉曼光谱的四种不同的散射频率差（不考虑耦合引起的微扰的话），也即每种对应一条斯托克斯线和一条反斯托克斯线。除了a模式是对称的之外，其他三种模式都是反对称的。

进行计算前，先引入导出极化率张量：

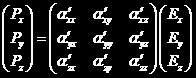
它联系着极化矢量和电矢量，。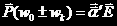

对同一个体系，坐标系不同，极化率张量各分量也会发生改变，但有两个不变量

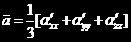
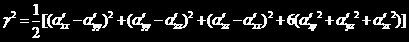
通过这两个不变量，可以得到退偏度的理论计算结果。

例如，对于振动模式c，有

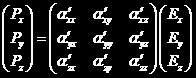
由于CCl4分子和振动模式的对称性，绕z轴（设振动平面平行于z轴）转动180度后，极化率张量不变，振动方式反向，所以对于P和E，有，。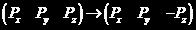

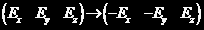这样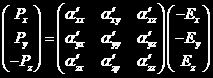，由于E为任取的，所以可得到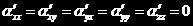，故

，

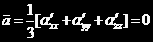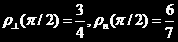
同样可以推得对于振动模式b、d，一样有。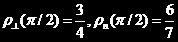

而对于对称振动a，由于分子对称性和振动对称性是一致的，所以显然有

，

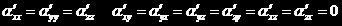那么

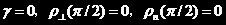
再加上上面已知的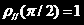，我们就得到了CCl4的几种特殊情况下的退偏度的理论结果。

实验步骤设计

1、实验仪器的设计

实验仪器图示如下

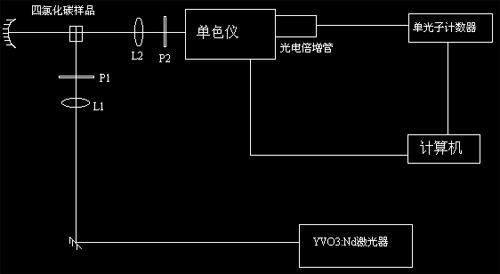
其中，L1,L2是聚光透镜，P1,P2是偏振片，整个实验装置除了偏振片之外都是原来拉曼光谱实验中已有的设备，不需要再另外添加（如果要测量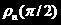和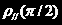则还需要再加一块1/2波片）。

2、实验步骤

（1）调节好拉曼光谱仪和各项参数，使得入射狭缝的光强最强，并且噪声较小。

（2）将偏振片P1放置到相应位置，调节角度为0度，使入射光经起偏后对于散射面为垂直偏振光。

（3）将P2放置到相应位置，调节角度为0度，使散射光对于散射面为平行偏振，启动软件进行一次500～560nm的单程测量。

（4）将P2角度调整为90度，使散射光对于散射面为垂直偏振，再进行一次相同范围的的测量。

（5）将调整P2前后得到的图象和归峰数据整合到一起进行比较，利用公式算出各峰的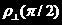，并与理论计算值比较。

（6*）加上1/2波片，使得快轴的方向与入射光透射方向成45度（即使得入射光偏振方向旋转90度成为平行偏振光），重复（3）（4）（5）。

（7*）取下P2，P1不变，让1/2波片的快轴方向与入射光透射方向平行，进行一次500～560nm的单程测量；然后将1/2波片旋转45度，再进行一次同样的测量，将两次结果进行比较并利用公式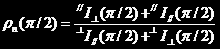计算出。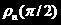

3、一些说明

由于实验中用的激光是近乎于线偏振的，所以不能直接做自然光入射时的测量，需要用（7）中的方法得到自然光入射的结果；在测量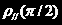时也不能直接就将P1置于90度上，这样会导致入射光强太小，测量结果的误差严重增大，所以需要一个1/2波片来调节线偏振的方向。

实验结果

由于实验的时候，开始没有1/2波片，后来拿到波片以后又因为操作不当，以致于没有得到正确的结果，因此只有对于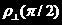的测量结果。

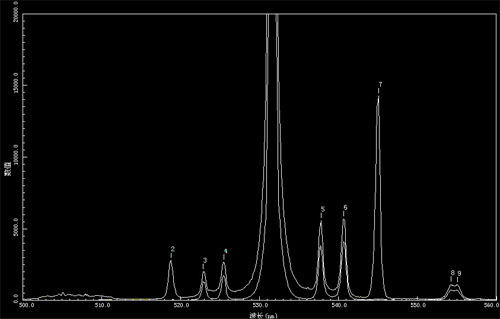
下面是将两次结果叠加的图象：

各峰的数值和退偏比：(对波长和最后两个峰的数值取平均，第一个峰因为误差较大没有计算)

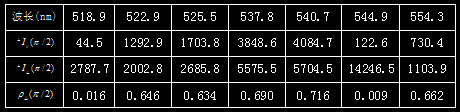
可以看到，实验测量的结果和理论的符合还是比较好的，波长为518.9nm和544.9nm的拉曼散射谱线对应的就是CCl4的a类对称振动模式，而其他谱线对应的则是非对称模式的振动。但是也可以看到，对应于非对称模式，测量所得得退偏比数值比理论计算得到的偏小，究其原因可能有：

1）偏振片没有固定，且实验中完全依靠目测判断偏振的角度，对准确性有一定影响。

2）仪器存在吸光和反射，影响了测量所得数值的准确性。

3）杂散光的干扰，增加了本底噪声。

4）对于不同偏振状态的光，单色仪的效率不同。

5）实验中的操作失误。

总结与建议

可以看到，对于拉曼光谱的偏振特性的测量，实验方法上是比较简单的，在原来实验的基础上稍加改动即可实现，而其中体现的物理思想又很有价值，因此我建议将这一实验加入拉曼光谱实验中，这样可以丰富并完善拉曼光谱实验的内容，并且也有利于实验者更加深刻地理解拉曼光谱的重要意义。