摘要

介绍一种确定椭圆偏振光主轴方向的方法，对椭圆偏振光主轴取向的规律进行分析和讨论。

关键词

椭圆偏振光，主轴，波晶片

引言

在《光学》中我们已经学过了有关光的偏振态的知识，而且在本实验室里也作了偏振光的实验，有些同学在前面做的“椭偏仪”的实验中也有用到光的偏振态的知识，相信大家对光的各种偏振态不会太陌生。其中椭圆偏振光是光的一种很重要的偏振态，而且如何区分各种偏振态的光是个非常典型的问题。我们知道仅仅利用偏振片只能将光分为三类：线偏振光；自然光源和圆偏振光；椭圆偏振光和部分偏振光。要区分自然光源和圆偏振光以及椭圆偏振光和部分偏振光还需要借助于1/4波晶片。而在利用1/4波晶片和偏振片区分椭圆偏振光和部分偏振光的过程中，非常关键的一步便是确定椭圆偏振光的主轴方向（也就是椭圆偏振光经过偏振片后产生光强极大或极小的偏振片透振方向），然后再使1/4波晶片的光轴和偏振片的透振方向与之严格平行，接下来再进行区分。在下面介绍了一种确定椭圆偏振光主轴取向的方法，并对椭圆偏振光主轴的取向规律展开了些许分析和讨论。

正文

椭圆偏振光是由频率相同、光矢量振动方向垂直、位相差恒定以及传播方向一致的两束线偏振光叠加而成的，其矢量方程可以表示为：

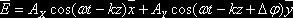     (1)

若将方程（1）中的参数消去，便可推得椭圆偏振光的轨迹方程为：

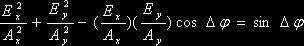     (2)

方程（2）表示的是一个主轴取向为的椭圆，如图1所示。以下为具体的分析和推导。

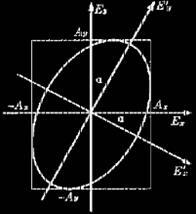
图1  椭圆偏振光的主轴取向

 

n        椭圆偏振光主轴方向的确定

图1所示的椭圆，其主轴与轴成角，实际上就是这个椭圆偏振光的光矢量轨迹在其波面上的投影图。因此，在椭圆主轴方向上应满足方程：

最大值     (3)

对方程(3)进行全微分将得到：

     (4)

联立方程(2)和(4)就可以推求得到：

     (5)

考虑到，将其代入(5)就可以得到：

     (6)

最后，通过求解方程(6)便可以得到椭圆偏振光主轴的取向角：

     (7)

n        椭圆偏振光主轴大小的确定

方程(2)表示椭圆偏振光轨迹的标准方程为：

     (8)

方程(8)表示的椭圆的长轴和短轴分别为：

     (9)

     (10)

结论

由方程(7)、(9)和(10)可以知道:椭圆偏振光主轴取向以及其长、短轴的大小分别取决于参与合成椭圆偏振光的两束线偏振光的振幅 、和位相差。其中，前者取决于入射的单色线偏振光的光矢量振动方向与波晶片光轴方向之间的夹角；而后者由入射的单色线偏振光波长和波晶片的性质与几何参数等决定。

下面讨论几个特例：

(1)     若，有方程(7)可以计算出，再由方程(9)和(10)分别可计算得和。于是此椭圆偏振光的方程可以表示为：

     (11)

此方程表示的是一个标准的正椭圆。

当时，同时若当时，同时若，则有，而此时由方程(7)可以推得可取任意值，再由方程(9)和(10)分别计算得到:和。由此可以知道这时椭圆偏振光的方程退化为

                 (12)

这一方程表示的是一个半径为的标准圆，此时为圆偏振光。

(3)若令，而则取不等于的任意值，那么由方程(7) 可推得椭圆偏振光主轴的取向角始终保持定值，即。再由方程(9)和(10)可分别计算出和。则这个椭圆偏振光的轨迹方程为:

     (13)

由上一方程容易可看出，此时的椭圆偏振光的轨迹形状完全取决于参与合成椭圆偏振光的两束线偏振光之间的相位差 。

参考文献

(1)姚启均原著。光学教程[M]北京：高等教育出版社（第三版），2002