引言

八十年代以来，“PLD”（脉冲激光沉积）技术制膜得到很大应用，引起人们较大兴趣。

实验 [张树东等，激光烧蚀Al靶产生的等离子体中辐射粒子的速度与激波，物理学报，Vol.50,No.8, 1512，2001] 指出：

功率密度~10¹⁰ w cm^-2

波长λ=1060 nm

脉宽t=10ns

激光打在Al靶上，观测到Al I，II，III发射谱线，其中，

很强，本文试图解释之。

 

近似与模型

w₀/w = 2.7，不在共振区，半经典近似过不去，必须用全量子方法。模型取为孤立Al原子与光场的作用，且只考虑

二能级间跃迁，不考虑其他能级，作粗略估算。

 

理论计算

相干态近似（汪克林等提出），考虑到三阶，光场与孤立Al原子系统的波函数为：

|α>是光场相干态，有

|α>=Exp[αa⁺|0>]

a|α>= α|α>

由相干态近似法f₁+g₁=0

系统的哈密顿量H=H_A+H_L+H_AL，原子的哈氏量H_A，光场H_L，相互作用项H_AL，由光场的二次量子化可知H_L，H_AL

是单，双，三光子与原子作用的耦合常数。

取到三阶，主要基于

w₀/w=2.7

由Schrōdinger Equ.

可得到系统的演化方程

要求Hψ，利用

由此可展开Hψ，对应a+j(j=0,1,2,3)项的系数相等，可得到方程组：

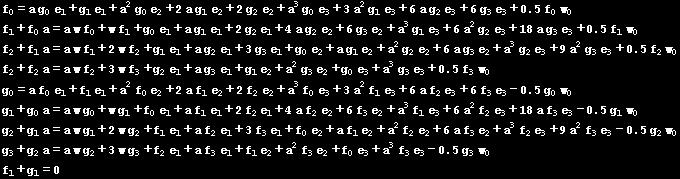
求解线性方程组，得到系统演化的常微分方程组，

过于繁琐，不再列出。

计算处于上能级几率P : P=A/B

求B只需将上式中“f”换为“g”

数值求解系统演化的微分方程时：

w₀=4.78*10¹⁵HZ

w=1.77*10¹⁵HZ

初值除g₀=1,其他f_j,g_j(j=0,1,2,3)为0

步长h=10^-18s,作了10⁵次迭代，

即算到了t=10^-13s

 

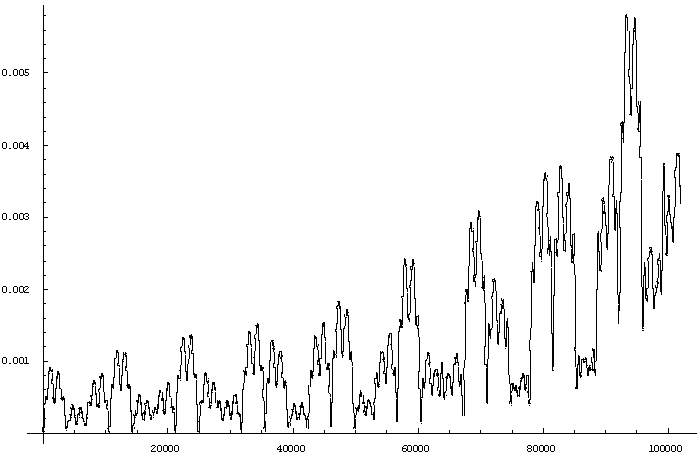
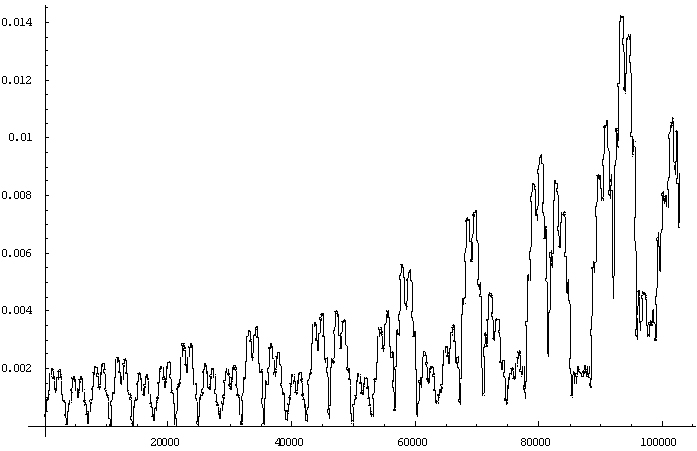
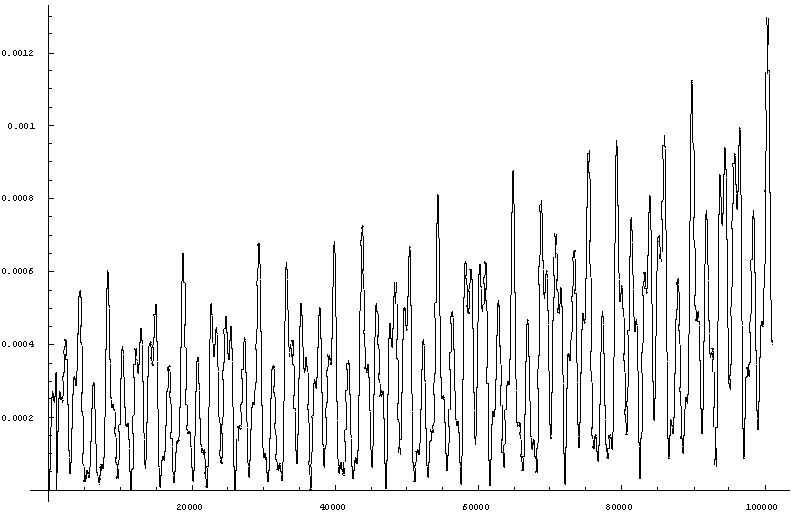
结论与问题

n        有较大几率（0.5ω，1ω，0.1ω）处于上能级，这也许正是发射谱线的来源。但几率又不是太大，处于电离态的原子 更少（实验也证实了这一点）。由此,喷溅气体的等离子特性并不明显，理论处理 “PLD”喷溅时可用热模型

n        耦合常数较大或光子数较大时几率较大

n        单个原子几率p 剧烈震荡，且峰在生高

n        10^-13 s <t< 10^-8s,p如何变化？

n        功率密度与所取初值如何联系？即上面α取2.0，2.5的理由何在？

n        直观感觉，峰是单，双，三光子三种作用之一的峰？耦合常数较大时有接近的双峰出现 ，两种作用相当的结果？

n        从能带与表面物理角度更仔细考虑，结果如何？

总之 采用三阶相干态近似，并考虑了三光子吸收，理论上计算了的跃迁几率，解释了实验中观测到的跃迁，为类似计算提供了一个范式。