γ射线的吸收

n        实验目的：验证γ射线通过物质时其强度减弱遵循指数规律，测量γ射线在不同物质中的吸收系数，估计γ射线的能量。

n        实验原理：当γ射线穿过物质时，与物质作用发生光电效应、康普顿效应和电子对效应（当γ射线的能量大于1.02MeV），γ射线损失其能量，γ射线与物质的原子一旦发生上述三种相互作用，原来为Eγ的光子就消失，或散射后能量改变并偏离原来的入射方向。γ射线通过物质时其强度会逐渐减弱，这种现象称为γ射线的吸收。单能窄束γ射线强度的衰减遵循指数规律：

I=I₀exp{-μd}

其中I、I₀分别是通过物质前、后γ射线强度，d是γ射线通过物质的厚度（单位为cm），μ是物质的线性吸收系数，μ的大小反映了物质吸收γ射线能力的大小。

n        实验仪器：NaI闪烁体计数器，放射源Cs-137, 铝片、铜片、铅片各若干，游标卡尺等。

n        实验步骤：

1.        本底测量，关闭放射源射线出口，重复进行三次本底测量，取平均；

2.        用游标卡尺量出每一片铝片的厚度；

3.        打开放射源射线出口，每次在出口处加入两片厚度以知的铝片，记数，测三组数据取平均；

4.        对铜片和铅片重复上述的2，3两步。

n        实验条件：放射源Cs—137;统一测量时间10s；本底值测量 (162+164+154)/3=160；无屏蔽物测量记数(64285+63962+64866)/3=64374

 

铝片对该γ射线的吸收系数的测量：

n        实验数据：

 

其中d为所加金属片总的厚度，I₁ ，I₂ ，I₃ 分别为三次重复的测量值。

n        测量曲线：

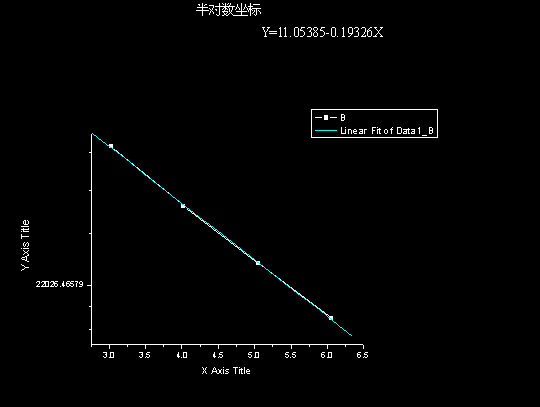
n        数据处理

l        计算得到铝片对该能量的γ射线的线性吸收系数为 μ_铝=0.19326/cm,

l        折合成铝片对该能量的γ射线的质量系数为0.0717cm2/g

l        查表估计出该γ射线的能量在0.60—0.80MeV之间

 

铜片对该γ射线的吸收系数的测量

n        实验数据：

 

其中d为所加金属片总的厚度，I₁ ，I₂ ，I₃ 分别为三次重复的测量值。

n        测量曲线：

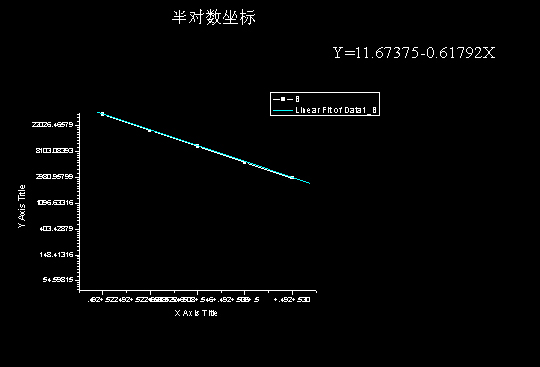
n        数据处理

l        计算得到铜片对该能量的γ射线的线性吸收系数为 μ铜=0. 61792/cm

l        折合成铜片对该能量的γ射线的质量系数为0.0695cm2/g

l        查表估计出该γ射线的能量在0.60—0.80MeV之间与上面估计区间一致

 

铅片对该γ射线的吸收系数的测量：

n        实验数据：

 

其中d为所加金属片总的厚度，I₁ ，I₂ ，I₃ 分别为三次重复的测量值。为了减小测量的误差，括号中的测量时间有所改变。

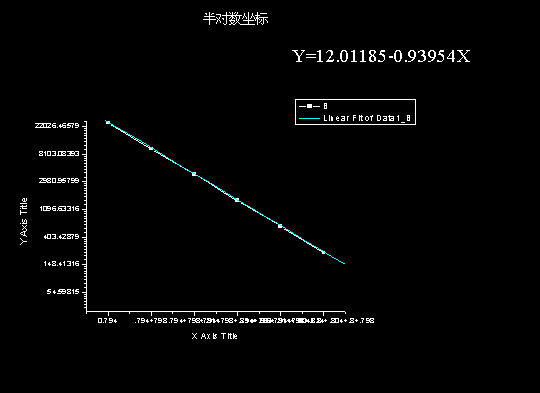
n        测量曲线：

n        数据处理

l        计算得到铅片对该能量的γ射线的线性吸收系数为 μ_铅=0. 93954/cm

l        折合成铅片对该能量的γ射线的质量系数为0.0829cm2/g

l        查表估计出该γ射线的能量在0.80MeV附近 与上面估计区间稍有偏差

 

实验结论

n        从标准表中查到该γ射线的能量应介于0.60 MeV 和0.80 MeV之间。下面给出标准值：

n        通过实验，我们可以发现不同的物质对γ射线的吸收能力是不同的,实际上即使是同一种物质，它对不同能量的γ射线的吸收能力也是不同的。在相同的厚度条件下，铅对γ射线的吸收能力大大高于其他两种材料，这也正是铅服用来防护γ射线辐射的原因。

 

结论分析

n        光电效应：当一个光子和原子相碰撞,它可能将自己的全部能量交给一个壳层电子(主要是K壳层),使电子脱离原子而运动,光子本身则整个被吸收,这种现象就称为光电效应.光电效应的线性吸收系数μ_r ∝ NZ^4－5/E^3.5; μ_r的大小直接反映了光子在通过单位距离物质时，产生光电效应的几率。

n        康普顿效应：光子和原子中的一个电子的弹性相互作用。康普顿效应的线性吸收系数μ_e ∝NZ/hυ[ln(2 hυ/m_ec²)+1/2]，与Z成正比，γ射线的能量越大， μe 越小。

n        电子对效应：当光子的能量大于两个电子的静止质量（1.02MeV），在原子核库仑场的作用下，入射的光子可以完全被吸收，产生一个正负电子对，电子对效应的线性吸收系数μK ∝N²ln(2hυ)

 

验证泊松分布

放射性元素的衰变一般不受外界物理化学条件的影响。它服从一定的统计规律。在一定的时间原子核的衰变率和能衰变的原子核数目成正比：

dN/dt= -λN

λ是衰变常数，它的意义是平均寿命。积分可得：

N=N₀exp(-λt)

在一个短的时间间隔内观测，衰变数服从泊松分布，本实验就验证了这一点。

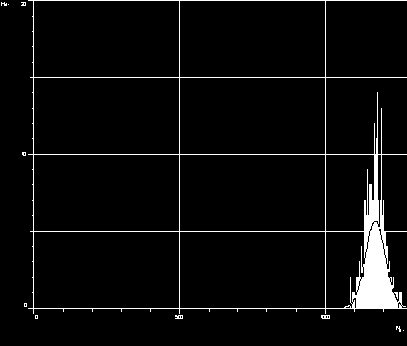
n=485    μ=1172    σ=30

实验结论：放射性元素衰变的统计分布规律--泊松分布产生的原因是原子核的衰变是一种随即的过程，上述实验结果也恰恰反过来证明了原子核的衰变是一种随即的过程。

 

放射性元素衰变泊松分布的成因和γ射线的科学应用

n        泊松分布的成因：

泊松分布是最重要的离散型分布之一，它多是出现在当随机变量表示在一定的时间或空间内出现的时间的个数这种场合，且任意时间或空间事件的出现与否是随机的。放射性元素的衰变的统计就是符合上述要求的。我们把每一秒分成等长n段（n是一个很大的自然数），表示为l₁,l₂,……l_n。假定：

[1]在每一段l_i内，恰发生一次衰变的概率，近似的与这段时间之长（1/n秒）成正比，即可取λ/n；又假定1/n很小，在l_i内发生两次或者更多的衰变是不可能的。因此在l_i内不发生衰变的概率是1-λ/n。

[2]l₁,l₂,……ln各段是否发生衰变是独立的。

把在[0,1]时段内发生衰变的次数X视作在n个小段l₁,l₂,……ln内有衰变发生的时段数，则按照上述[1]和[2]的假定，X应服从二项分布B（n,λ/n）.于是P（X=I）=CⁱN(λ/n)ⁱ(1-λ/n)^n-1.当n趋于无穷大的时候, CⁱN/nⁱ趋于1/n!，(1-λ/n)n趋于e^-λ.所以可以得到放射性元素的衰变符合统计中的泊松分布，反过来有泊松分布也很好的说明了放射性元素的衰变是随机的。

n        γ射线的科学应用：

任何一门科学或一项技术都有其实际生活生产中的应用，γ-射线技术更是在很多领域展现了巨大的实用价值：

l        医学上的应用：γ射线成像是一种实用技术，能帮助医生诊断疾患，如癌症等。但是，如果要想使γ射线照相在临床中得到应用，就必须克服其分辨率低(标准探测器件探测不到小于1cm的肿瘤)和体积庞大的缺点。Thomas Jefferson国家加速器实验室(Jefferson Lab)的科研人员利用Hamamatsu公司生产的光电倍增管，研制出一种精巧的γ射线照相机，它非常适合于胸部成像使用。专为胸部和小动物成像设计的这种成像器件，视场范围在2×2 in²～8×6 in²。设计分辨率已提高到2mm。γ刀在治疗脑瘤方面也有其无可比拟的效果。

l        γ射线料位计和探伤仪：γ射线料位计常用作料位开关。工作原理是在料库的一侧设置同位素源,在另一侧设置探测器,同位素源向探测器定向发射γ射线,若库内料面低于它,探测器检测得出料空信号;若库内料面高于它,则物料遮挡、吸收γ射线,探测器检测得出料满信号。γ射线料位计的特点是日常运行维护工作量小，操作简单，但也存在γ射线料位计放射源污染环境，放射源的衰减使料位控制不可靠等不足。γ射线探伤机又是γ射线最为广泛和普遍的应用之一。

γ射线料位计

l        γ射线天文学应用：线天文学是利用波长短于0.01埃的辐射来研究天文现象的学科。γ射线被地球大气严重吸收，因此只能利用高空气球，火箭和卫星搭载仪器进行观测。能量高于千亿电子伏特的甚高能γ射线穿过地球大气时会产生高能粒子簇射，从而形成切连科夫辐射。可以用特殊的大口径望远镜来探测这种辐射而间接探测到γ射线源。

l        γ射线生物学应用：γ射线人工诱导植物及微生物基因突变，从中筛选出对人类更有应用价值的新品种。

l        γ射线军事应用：在尽可能小的对建筑产生破坏的情况下，对生命体造成无法愈合的损害甚至杀死生命体。