基本原理

n        天然放射性物质放出的α粒子，能量范围是3-8MeV,在这个能区内，α粒子的核反应界面很小，因此可以忽略。

n        α粒子与原子核之间虽然有可能产生卢瑟福散射，但几率很小。

n        α粒子与物质的作用主要是与核外电子的作用，作用之后将使原子电离、激发而损失能量

入射粒子与核外电子作用而传给电子的最大能量

当M为氦原子核，m为电子时，可见Emax=5.45x10^-4E₀<<E₀

因为只有Emax超过电离电位I₀时,电子才能摆脱原子而电离

n        所以入射粒子产生电离的最小能量为:

Emin=(m+M)²I₀/4mM

在充满空气的电离室,入射粒子为α粒子时空气中氧的电离电位最小,I₀=12.2ev,Emin=22kev;入射粒子为电子时,Emin=12.2ev。电离后产生的电子和正离子，只要它们具有的能量超过Emin，也同样能产生电离。

 

电流电离室的结构

n        电流电离室的输出脉冲讯号用弱电流（直流）放大器来测量粒子的平均电流（或电压）

n        下图给出了圆柱型电离室结构图。在一个充气容器（屏蔽壳或压力壳）内，安装一对相互绝缘的电极，与测量电路联结的那个电极称收集电极（阳极），收集电极通过负载电阻（RL）与高压电源（HV）正端（正高压电源的正端或负高压电源的地端）相联，另一电极称高压电极相应接电源负端（地或负高压电源负端），以保证电子的收集。在收集电极周围还有一个保护环，它的电位与收集电极电位接近，一般直接接高压正端。收集电极、高压电极和保护环都要用高质量的绝缘体来固定，并使它们彼此绝缘起来。

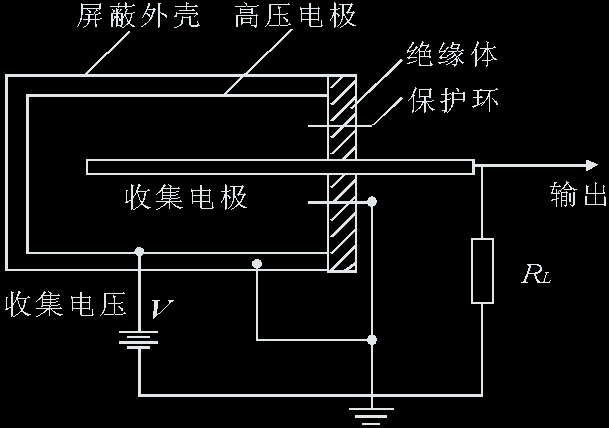
图1  电流电离室的结构示意图

 

电离室的工作原理和饱和特性

n        当带电与不带电的粒子进入电极空间时，直接或间接的引起气体电离。若极间无电场，正负离子对经漂移而终致复合，电离电流为零。

n        若在两极间加电压V，则离子在极间电场作用下向两电极移动（正、负离子移动的方向相反），产生电离电流I。V较低时，场强弱，离子速率小，一些离子在达到电极前复合，电极不能收集到全部电离电荷。提高V，场强增大，离子复合机会减小，将会有更多的离子到达电极。当场强使离子速率高到正负离子很少复合时，则电离电荷几乎可全部被电极收集，这时电离室开始工作在饱和区，相应的电压V₀称为饱和电压。

图2  电离电流与极间电压的关系

 

n        使用电离室时，应将电压选取在饱和区内，即图中曲线的平坦区域。令n为每秒进入电离室的粒子数，产生的离子对数为N，每个粒子消耗的平均能量为E，产生一对离子所需能量为ε，那么所形成的平均电离电流，即饱和电流为：

I₀ = Ne = n(Ee/ε)

这个电流范围是很宽的，在10-3A到10-16A之间，由入射粒子流强度而定，经常是很微弱的。例如，一个空气电离室，设入射α粒子能量为5.3MeV，n =4×3.7×10⁴个/s，如果α粒子能量全部损失在电离室中，则电离电流为3.5×10^-9A。

 

实验仪器

n        电流电离室

n        电流放大器                                           10^-9A

n        分析万用表                                           3V(DC)

n        高压电源(10KV)                                   1KV

n        收集探头

n        Am-241放射源

l        放射体类型                                    主要是α射线，也有γ射线及转化电子

l        α的衰变能量                                 约5.5MeV

l        半衰期                                            458a

l        α的衰变能量的衰变                     8MeV

l        衰变产物的半衰期                        2.2×10⁶a

l        γ的能量                                         59.5KeV

l        活度                                                340×10³Bq(约9μCi)

 

实验步骤及内容

n        如下图连线.

n        取出Am-241放射源并插在收集极上。

n        用游标卡尺测量从放射源顶部到电离室底板的距离d

n        先使电离室活动内盖压在放射源上,

n        使游标卡尺靠紧桶壁,测量从外壁上沿到电离室活动内盖的距离,定为S.

n        以后每次测量S减小2mm,同时d就相应的增加了2mm

n        对电离室加饱和区内的某一电压(约1KV).

n        从d~2mm开始,将d值记录下来.

n        从分析万用表上读数,乘上放大器上的量程倍数,即得相应的产生电流值.

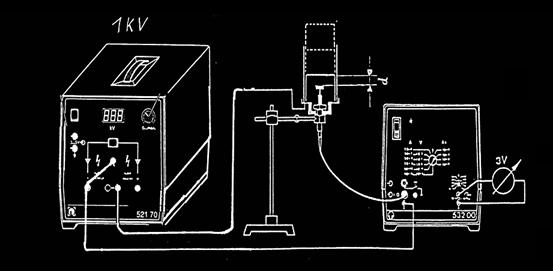
图3  实验装置连接图

n        产生电流值I随放射源顶部到电离室底板的距离d变化的数据

 

 

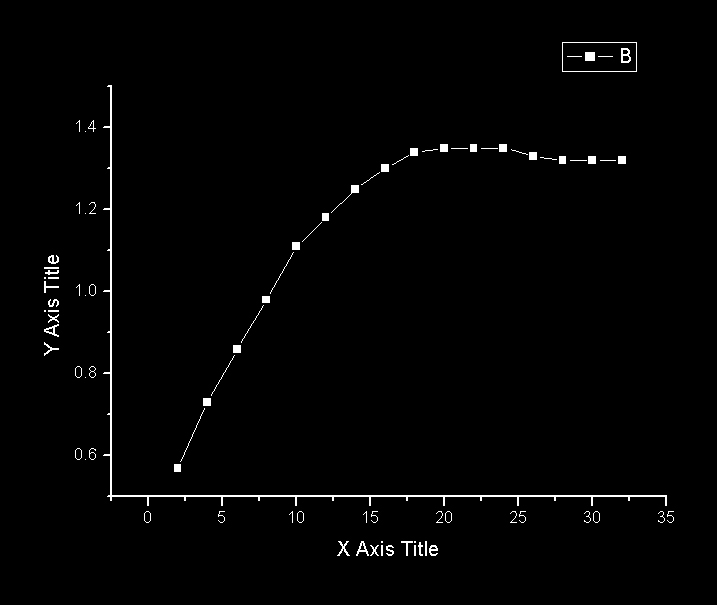
图4  I-d函数曲线

 

实验结果分析

据图所示，α粒子在空气中的射程R≈21mm。d<R时，I随d值增大而增大，慢慢趋于平缓，这是可以理解的；但是当d>R时，I却随d减小而减小，最终趋于平缓，斜率在10^-2量级。这似乎有些反常，现重点解释这一段反常曲线

n        带电粒子在外电场下的运动——漂移

l        漂移在漂离过程中电子和正离子在外电场中被加速，又和气体分子碰撞，损失能量而减速，不断加速和减速的结果宏观上表现为他们具有一定的平均速度w—漂移速度。假设每次碰撞后电离粒子的动量全部损失的话，就可导出：

E为电场强度，P是气体压强，m为电离粒子的质量，λ是它在1atm下的平均自由程，u是它在电场下的混乱运动的平均速度—激活速度。eE/m是在两次碰撞之间（即λ/P）电离粒子的加速度，λ/uP为走过λ/P路程所需时间，μ为迁移率。

l        激活速度u可以用平均激活能η表示，η是电离粒子混乱运动的能量在有电场比无电场时所增加的倍数，即有关系式：

对重粒子来说，η≈1，电子~102

E/P较小时，电子的漂移速度大约在105~106cm.s-1;离子在102~103cm.s-1,比电子小三个数量级。

l        那么，当d增大时，E将减小,w也减小，电子和正离子混乱运动可能将加剧，将会产生以下结果：

a.         电子吸收：电子被中性气体俘获，形成负离子。

b.        复合电子和正离子复合形成中性分子,负离子和正离子复合成中性分子。

n        电子吸附

l        电子被俘获形成负粒子后，其漂移速度大大减慢，同时又会增加粒子复合的可能性，从而导致收集到的电离数N减少，这对测量是不希望的。

l        电流电离室内充空气，氧被吸附的几率h~10^-4，d取10mm时，而电子在运动过程中碰撞次数约为(0.3~1)×10⁵次,电子基本被吸附了

 

n        复合

l        单位时间，单位体积内正负粒子复合数目为：-dn+/dt=-dn-/dt=αn+n-

l        α为复合系数。离子和离子的α为10-6 cm³ s-1数量级，电子和离子复合α为10-7~10-10 cm³ s-1, 由上页可知主要发生离子和离子复合，当V取0.18mL(即d=20mm时)，α取10-6 cm³ s-1，n为1.5×105个，斜率在10-2量级