测电子荷质比
在实际的实验中为了测量电子的荷质比，需要测一定B值下进行摄谱，进而用阿贝比长仪测圆环的半径，难度较大，我们在实验中测量了相邻谱线的不同重合下的B值，能否通过这些不同的B值直接求出荷质比，下面我们就来考虑这个问题。
现在我们想仅通过在不同磁场条件下干涉环重叠情况来求得电子荷质比。根据原子物理的知识，这九条谱线的间隔用波数差表示为
，其中
。如下图：
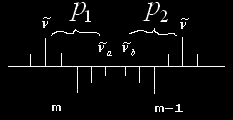
设中心谱线的波数为
，m级中距中心间隔为
p1
的谱线波数为
，（m-1）级中距中心间隔为
p1
的谱线波数为
，则
当的m级与的（m-1）级重合时，由
且在角度很小时
则
其中d为F-P标准具的间隔。
即
(1)
若设m级中与中心间隔为p的波数差为
，则
。
将(1)代入上式，得：
其中p1、p2分别代表它们距各自中心的间隔，随着重叠情况的不同，p1+p2的取值也会不同。
例如，当重叠部分为五条线时，p1= 4，p2= 4，
当重叠部分为四条线时，p1= 4，p2= 3，
当重叠部分为三条线时，p1= 4，p2= 2。
从另一方面来看，
这表示
是随着B的变化呈线性变化的。
将上式变一下形，即得
也就是说，不同的重叠情况对应了不同的
值，只要我们测出相应的B值，就可以拟合出k，进而由
求出电子的荷质比
。
下面我们来讨论k的拟合问题。
若我们根据
这一正比例关系，由每一组的
值分别得到一组k值，再求出平均值的方法可以得到如下结果：
将k=27.422代入公式
，可得
，而理论值为1.758E+11，相对误差Dd =17.5%，我们认为这是由于实验中值的系统误差造成的，所以我们改用线性拟合的方法，得出拟合曲线：
作出拟合曲线：
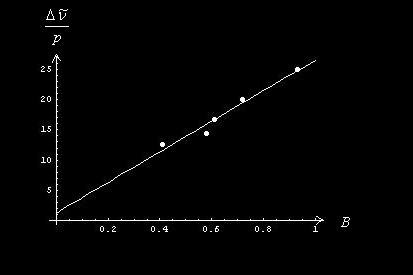
取 k=25.336，代入公式
，得
，相对误差Dd =8.5%，虽然还不是很理想，但比测量干涉环的直径的方法要简单的多。分析起来，实验中用电流来标定的磁场值有一定的范围，再者，我们是用眼睛来观察干涉环的重叠情况，不太准确，造成误差。
确定g因子，及能级量子数L,S,J
塞曼效应是一个伟大的实验，它是研究原子结构的重要实验方法之一，实验内容上不应只局限于测电子荷质比，我们可以运用原子物理知识和实验数据确定g因子，及能级量子数L,S,J, 得出谱线是由哪两个能级跃迁产生的。
根据实验中观察到的s线和p线的条数，利用选择定则：
DM=0，产生p线
DM=±1，产生s线 （注：DM是DMj的简写）
且M=J，J-1，…，-J
由此可以确定上下能级分裂的层数，进而确定J和M的取值。
实验中观察到谱线分裂成三条p线和六条s线，现假设两原子态分别为：（1）和（2），令其磁量子数、总角动量量子数、轨道角动量量子数、自旋角动量量子数及朗德因子分别M1，J1，L1，S1，g1和M2，J2，L2，S2，g2。
由三条p线根据选择定则：DM=0，推出（1）、（2）态中一个态的磁量子数共有三个值，设为（1）态，其能级分裂为三层，故：
2J1+1=3
J1=1，M1=0，±1
由六条s线，推出：DM=±1，（2）态能级分裂为五层，即：
2J2+1=5
J2=2，M2=0，±1，±2
根据塞曼效应波数计算式：
其中
是洛仑兹单位。
能级分裂图
若g1>g2，九条谱线按其与原谱线的波数差从大到小排列得：
上式中前后项相减得：
由测得的数据，各相邻谱线裂距相等，即：
因为(g1-g2)L=Dv’
，(Dv’为两相邻谱线波数差)，所以：
若g2>g1，同理可得：
若g1=g2，不符合实验现象，舍去。
以上推导得出两组g1，g2值，取舍由量子数L的取整性质决定。根据L-S耦合时，能级跃迁的选择定则DS=0推出：S1=S2。又因为：J1=1，J2=2，且J1，J2只能为0或正整数，而J=L+S，L+S-1，¼，|L-S|，又Hg有两个价电子，推得：S=0，1，但
将S1=S2=0代入上式得：g1=g2=1。与g因子推导结论不符，舍去。所以S1=S2=1。
下面求L，由：
将(1)，(2)代入(3) 式得：
分别将DL=0，±1代入（4），（5）式，（5）式无满足条件的解，舍去。由（4）推得：L1=L2=0。g1，g2值由（1）式给出。又因为2S+1=3，故原子态（1）为3S1，原子态（2）为3P2。
小结
以上的讨论说明，我们可以通过对一谱线塞曼分裂的s线条数与p线的条数来确定谱线是由哪两个能级跃迁产生的，但有一前提条件，我们必须事先知道原子的种类，以便由价电子数来确定S，所以我们还必须结合其它的仪器进一步分析。
