简介

自旋不为零的粒子，如电子和质子，具有自旋磁矩。如果我们把这样的粒子放入稳恒的外磁场中，粒子的磁矩就会和外磁场相互作用使粒子的能级产生分裂，分裂后两能级间的能量差为

ΔE = γhB₀                                     （1）

其中：γ为旋磁比，h为约化普朗可常数，B₀为稳恒外磁场。

如果此时再在稳恒外磁场的垂直方向加上一个交变电磁场，该电磁场的能量为

hν                                              （2）

其中：ν为交变电磁场的频率。

当该能量等于粒子分裂后两能级间的能量差时，即：

hν = γh B₀                                 （3）

2πν = γ B₀                                 （4）

低能极上的粒子就要吸收交变电磁场的能量产生跃迁，即所谓的磁共振。

 

实验设备

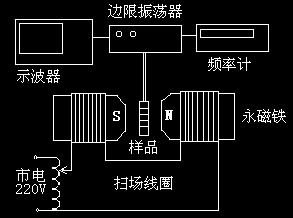
a)         样品水：提供实验用的粒子，氢（¹H）核。

b)        永磁铁：提供稳恒外磁场,中心磁感应强度B约为0.55T。

c)        边限振荡器：产生射频场,提供一个垂直与稳恒外磁场的交变磁场，频率ν。同时也将探测到的共振电信号放大后输出到示波器，边限振荡器的频率由频率计读出。

d)        绕在永铁外的磁感应线圈：其提供一个叠加在永磁铁上的扫场

e)         调压变压器：为磁感应线圈提供50周的扫场电压。

f)         频率计：读取射频场的频率。

g)        示波器：观察共振信号。

 

实验原理

本实验要测的一个物理量是氢质子的γ因子，由（4）2πν=γB₀可知，只要有B₀，ν即可求得γ，B₀在实验设备中已标定（如0.55T），ν可由频率计测出。

但是仅此γ是无法用实验求出的。因为两能级的能量差γhB₀是一个精确的量，交变电磁场的能量hν很难固定在这一值上。实际上等式hν = γhB₀ 在实验中很难成立。

一个好的办法是在永磁铁B₀上叠加一个低频交变磁场B_mSinωt（ω为市电频率50HZ，远低于射频场的频率,ν约几十MHZ），使氢质子两能级能量差的值γh（B₀+B_mSinωt）有一个变化的区域。我们调节射频场的频率ν，使射频场的能量hν进入这个区域，这样在某一瞬间等式hν =γh（B₀+B_mSinωt）总能成立。（见下图）

此时通过边限振荡器的探测装置在示波器上可观测到共振信号

由上图可见，当共振信号非等间距时，共振点处hν=γh（B₀+B_mSinωt），B_mSinωt未知。无法利用等式求出γ值。

调节射频场的频率ν使共振信号等间距，共振点处

ωt=nπ，     B_mSinωt=0，       hν=γhB₀

γ=2πν/B₀      γ值可求。（见下图）

 

探测装置的工作原理:图一中绕在样品上的线圈是边限震荡器电路的一部分，在非磁共振状态下它处在边限震荡状态（即似振非振的状态），并把电磁能加在样品上,方向与外磁场垂直。当磁共振发生时，样品中的粒子吸收了震荡电路提供的能量使振荡电路的Q值发生变化，振荡电路产生显著的振荡，在示波器上产生共振信号。

 

实验要求和步骤

1．观察¹H (样品水)的核磁共振信号：（记六组数据和图形）

a)         将边限震荡器盒上的样品小心地从永磁铁上的插槽放入永磁铁中。（注意不要碰掉样品的铜皮

b)        将边限振荡器的“检波输出”接示波器的“CH1”端，置示波器的“方式”为CH1。

c)        将边限振荡器的“频率测试”端接多功能计数器的“输入A”。

d)        将调压器插头接入220V市电插座。

e)         调节边线振荡器的“频率调节”旋钮，使示波器上出现共振信号。

f)         固定提供扫场的调压器输出电压为10---100V中的某一值,调节边限振荡器的“频率调节”旋钮改变边限振荡器的频率ν，观察示波器上共振信号的变化，任取三个不同波形画下，并记下相应的扫场电压V，变边限振荡器频率ν（由频率计读出）值。

g)        固定边线振荡器的频率ν，改变调压器的输出值V (<100V), 观察示波器上共振信号的变化，画下三个不同波形，记下相应的V，ν值。

h)        对共振信号波形随V，ν，变化的现象进行讨论。

2．测量¹H的γ因子和g因子：

a)         将样品放入永磁铁的磁场最强处，可左右移动边线振荡器铁盒，观察示波器上共振信号波形，当波形尾波最多时样品即在磁场最强处。记下此时标尺的刻度值。

b)        置示波器扫描时间为5ms/div,调节边线振荡器的“频率调节”旋钮使共振信号等间距（间隔为10ms）。

c)        读频率计记下此时的频率值。

d)        将信号调离等间距重复以上b--c步骤，此步骤进行六次。求频率的平均值。

e)         记下永磁铁上的磁感应强度B₀值。

f)         由公式计算g和γ因子

研究性内容/span>

(1)．比较纯水和加入少许 或 水溶液时的共振信号，观察顺磁离子对共振信 号的影响，并解释之。

(2)．用脉冲法重复上述实验。

(3)． 若已知 核的旋磁比 ，用扫场法测出调制磁场随其相位变化的关系曲线。

实验数据

测氢核的γ因子和g因子：

共振信号等间距时的射频频率：

 

频率的平均值ν：24.708MHZ

γ= 2πν/B₀ =2π×24.708/0.58 = 2.675×102MHz/T

g = hγ/2π×μN = 5.583