|
光强调制法测光速
光速是物理学中最重要的基本常数之一，也是所有各种频率的电磁波在真空中的传播速度．
历史上光速测量方法可以分为天文学测量方法、大地测量方法和实验室测量方法等。
1607年伽利略最早提出大地测量方法来测量光速．1676年， 丹麦天文学家罗默通过观察从卫星蚀的时间变化和地球轨道直径求出了光速．1728年，英国天文学家布莱德雷（1693—1762）采用恒星的光行差法测量了光速，这些是天文学测定的方法。
1849年，法国人菲索第一次在地面上设计转齿轮装置测定光速。 1850年，法国物理学家傅科设计了转镜法测出的光速是298000 千米/秒。另外傅科还测出了光在水中的传播速度，它小于光在空气中的速度，彻底否定了光的经典微粒说。
1928年，卡娄拉斯和米太斯塔德首先提出利用克尔盒法来测定光速。1951年，贝奇斯传德用这种方法测出的光速是299793千米/秒.
实验原理
可见光的频率为 的数量级，超出了所有仪器的响应。在本实验中光源是发光二极管。用50兆赫兹的高频正弦电压信号将光的强度进行调制，对强度调制光检波后就得到周期大大扩展了的电子学信号。发光二极管所发红光在仪器内调
制后，分为两路，一束输入到双踪示波器的X通道；另一束从出射孔射出，见图。出射光经过直角反射镜改变传播方向，从接收孔又进入到仪器内，输入到示波器的Y通道。这二个频率相同的强度调制波信号在示波器内相干，屏幕上得到李萨如图形。一般而言，这种图形是椭圆。如果两种信号之间的相位差为零或 ，李萨如图形为直线。对应于
相位差为零和为 的这两条直线应有不同方向，一个在一、三象限，另一个在二、四象限。这两束调制信号之间的相位差与出射光在空气中传播的距离有关。如果直角反射镜靠近出射孔时，两束信号之间的相位差相等（可通过调节仪器上的相位旋钮做到），示波器上得到一条直线。将反射镜移远的过程中，李萨如图形变化为椭圆。椭圆的方位
和椭圆度也随距离而改变。当示波器上再度出现直线时，说明示波器中Y分量相位改变了 。即这束调制光程变化了半个波长。考虑到光经过两次平面镜的反射，半个波长等于直角反射镜移动距离 的两倍，或写成 。已知调制频率 ，
即可得到光在空气中传播速度:
实验仪器
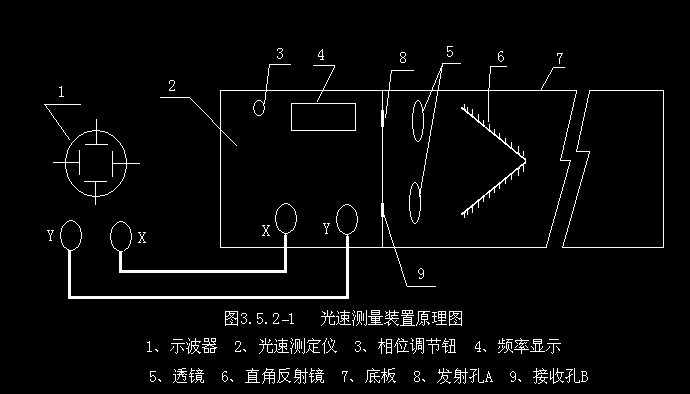
实验内容
1.测量光在空气中速度
（1）开启光速测定仪，将其两个输出端分别连接到双踪示波器X通道接口和Y通道接口。
（2）调节光路共轴
仪器上光的发射孔A和接收孔B外各有一个凸透镜，调节透镜位置，使发射孔处于其焦点附近。这样，光通过透镜后就大体上成为平行光了。在底板上前后移动直角反射镜，使得它反射的光经过另一个透镜会聚到接收孔B。为此，首先调节两个反射镜片背后的螺钉，使镜片垂直于底板且彼此成直角。其次，调节透镜的位置，使光线会聚到仪器的接收孔B。这样，在1.5米长的底板上前后移动直角反射镜，示波器上的李萨如图形都会发生变化，如果在底板远端移动反射镜时，图形无变化，说明光线尚未充分聚焦到接收孔，仍需继续调节光轴。
（3）完成了步骤2，反射镜在远端附近移动时李萨如图形呈椭圆，其大小与方位与的镜位置有关。这时可调节仪器上相位旋钮，令李萨如成为一直线。记录这时直角反射镜的坐标X1
（4）将反射镜向着仪器方向移动，注意观察示波器上的图形，椭圆会越来越大（为什么？），方向也逐渐改变。如果图形太大，可调节波器的电压灵敏度旋钮，使图形大小适当。当反射镜靠近接收孔时，波器的上的李萨如图形有成为一条直线，它的斜率应与开始时直线在不同象限。记录反射镜坐标X2 。当然，也可将反射镜从靠近仪器的位置逐渐移远，方向同上。
（5）计算出反射镜移动的距离，根据调制波的频率f ，按（1）式计算出光在空气中的速度。
2.测量光在水中的速度
将专用的1米左右的圆管内装满水，密封两端透明的盖子后，放在光路中。测量管长L。光经过管内的水照到放置在其后的直角反射镜。这时示波器上应有椭圆状李萨如图形。调节相位旋钮，使李萨如图成为一条直线。记录反射镜的坐标X1 。然后去掉水管，移动反射镜的位置，直至示波器上的图形又成为一条直线。记录此时反射镜的坐标X2 。这说明光强调制信号在空气中经过2倍|X1-X2| 的距离与该信号经过水中L距离产生的相位变化相等。根据（2）式计算水的折射率，根据（3）式计算光在水中的传播速度。
注意事项
仪器上光的发射孔A和接收孔B外各有一个凸透镜，调节透镜位置，使得光通过透镜后就大体上成为平行光， 再经过直角反射镜，使得反射光经过另一个透镜会聚到接收孔B。这相当于几何光学中的共轴调节，反射镜前后移动1.5米范围，李萨如图形应有变化。
开放实验
如何利用这种仪器还测量透明介质的折射率以及光在这些介质中的速度。
让光透过光路中一定长度L的某种透明介质，譬如水，先将示波器上图形调节为直线。然后移去液体，这时，示波器上图形为一椭圆。移动直角反射镜一段距离 ，直至示波器上又得到直线。这说明强度调制波在空气中 产生的光程变化（空气的折射率为1），
相当于波通过长度相等的空气与待测介质的光程变化。介质的折射率为 。根据 可以求介质的折射率。光在这种介质的速度为:
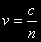
思考题
1. 红光的波长约为0.6微米。在空气中只走0.3微米就会产生 相位差。而我们在实验中确将直角反射镜移动了1.5米左右的距离，李萨如图表明两信号之间的相位，才改变 。这是为什么？
2. 光从直角反射镜的一块镜片被反射到另一块镜片，其间约为10厘米作用。而计算光速时确并未考虑到它。为什么？
3. 设水管两端的玻璃片厚度均为2毫米，玻璃的折射率为1.5。本实验中忽略的影响会对测量产生多大的误差？
|
