实验简介

材料的杨氏模量、切变模量以及断裂强度等宏观量都能反映出物质微观结构的特点。20世纪30年代，人们从物质结构理论出发，计算出的断裂强度值比实验值大几个数量级。这个重大矛盾迫使科学家提出了位错理论来解释实验现象。后来人们在电子显微镜下观察到了位错的形成和运动，证实了这种理论。科学的发展反复证明了时间是检验真理的唯一标准。

在这个实验中，用扭摆来测量金属丝的切变模量，同时要学习尽量设法避免测量那些较难测准的物理量，从而提高实验精度的设计思想。

 

实验原理

实验对象是一根上下均匀而细长的钢丝，从几何上说就是一个如图5.3.2-1所示的细长的圆柱体，其半径为，长度为。将其上端固定，而使其下端面发生扭转。扭转力矩使圆柱体各截面小体积元均发生切应变。在弹性限度内，切应变正比于切应力：

                       (1)

这就是剪切胡克定律，比例系数即为材料的切变模量。

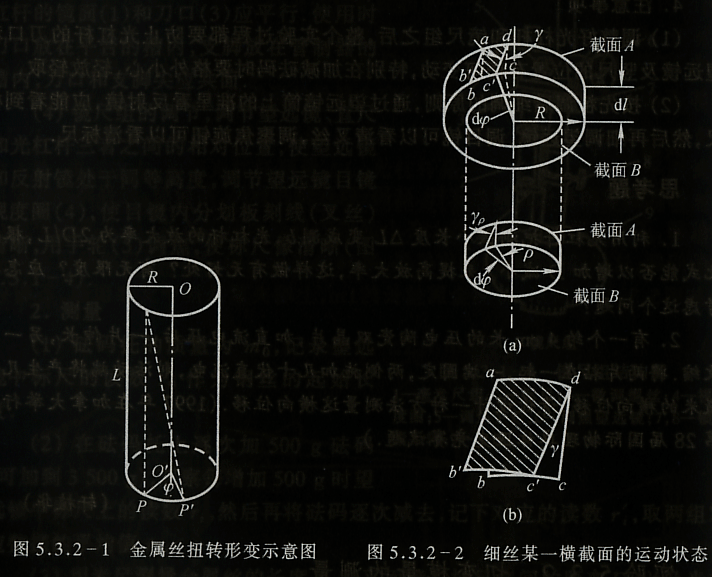
钢丝下端面绕中心轴线转过角（即点转到了的位置）。相应的，钢丝各横截面都发生转动，其单位长度的转角。分析这细圆柱中长为的一小段，其上截面为A，下截面为B（如图5.3.2-2所示）。由于发生切变，其侧面上的线的下端移至，即转过了一个角度， ，即切应变

                    (2)

在钢丝内部半径为的位置，其切应变为

                     (3)

由剪切胡克定律可得横截面上距轴线为处的切应力。这个切应力产生的恢复力矩为

截面A、B之间的圆柱体，其上下截面相对切变引起的恢复力矩为

                 (4)

因钢丝总长为，总扭转角，所以总恢复力矩

                       (5)

所以

                    (6)

于是，求切变模量G的问题就转化成为求钢丝扭矩（即其恢复力矩）的问题。为此，在钢丝下端悬挂一圆盘，它可绕中心线自由扭动，成为扭摆。扭摆过的角度正比与所受的扭力矩，

                    (7)

为金属丝的扭转模量。将式（7）代入式（6），有

                        (8)

由转动定律，

                   (9)

为摆的转动惯量，再由式（7）和（9）可得

                  (10)

这是一个简谐运动微分方程，其角频率，周期

                 (11)

作为扭摆的圆盘上带有一个夹具，这给测量或计算带来困难。为此，可将一个金属环对称地置于圆盘上。设环的质量为，内外半径分别为和，转动惯量为。这时扭摆的周期

                  (12)

由式（11）、（12）可得

                      (13)

               (14)

                 (15)

 

实验内容

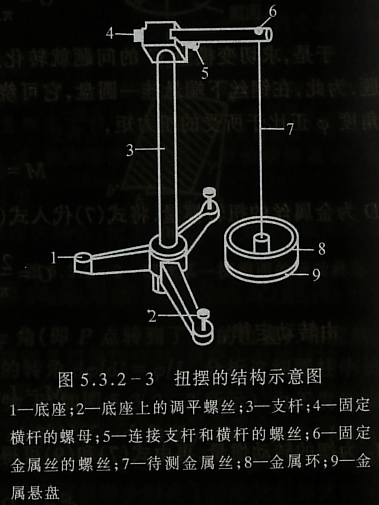
本实验用扭摆法测量钢丝的切变模量，扭摆装置如图5.3.2-3所示。

n        装配扭摆，使钢丝与作为扭摆的圆盘面垂直，圆环应能方便地置于圆盘上。

n        用螺旋测微器测钢丝直径，用游标卡尺测环的内外径，用米尺测钢丝的有效长度。

n        写出相对误差公式，据此估算应测多少个周期较合适。

n        计算钢丝的切变模量和扭转模量，分析误差。

 

设计性内容

n        换用不同直径的钢丝，重新实验。

n        改变钢丝扭转角度，从开始直到，每隔测量扭摆周期，并计算出切变模量，分析结果和原因。

实验重点

n        了解扭摆的特色和用途。

n        弄懂用扭摆测量金属丝切变模量的原理。

n        学习尽量设法避免测量那些较难测准的物理量,从而提高实验精度的设计思想。

n        实验前,钢丝要调直,圆盘要调平.钢丝长度为两固定端之间的距离,要测到凸柱的上表面。

n        保持圆盘绕中心轴转动,尽量避免有非切向的力使圆盘晃动。

 

思考题

n        试比较圆盘和圆环的质量,说明两者在质量相同之下,转动惯量不同的原因。

n        怎样测量任意形状的物体的转动惯量?实际测量时该怎样安排？

n        切变模量和杨氏模量同为表征物体力学性质的弹性常数,它们的物理意义有什么不同?它们之间有无联系？