实验简介
动量守恒定律和能量守恒定律在物理学中占有非常重要的地位。力学中的运动定理和守恒定律最初是从牛顿定律导出来的,在现代物理学所研究的领域中存在很多牛顿定律不适用的情况,例如高速运动物体或微观领域中粒子的运动规律和相互作用等,但是能量守恒定律仍然有效。因此,能量守恒定律成为了比牛顿定律更为普遍适用的定律。
本实验的目的是利用气垫导轨研究一维碰撞的三种情况,验证动量守恒和能量守恒定律。定量研究动量损失和能量损失在工程技术中有重要意义。同时通过实验还可提高误差分析的能力。
实验原理
如果一个力学系统所受合外力为零或在某方向上的合外力为零,则该力学系统总动量守恒或在某方向上守恒。即
 =
衡量 (1)
=
衡量 (1)
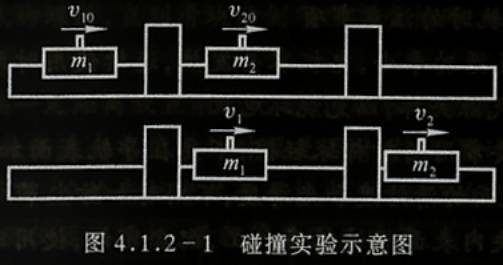
实验中用两个质量分别为 的滑块来碰撞(图4.1.2-1),若忽略气流阻力,根据动量守恒有
的滑块来碰撞(图4.1.2-1),若忽略气流阻力,根据动量守恒有
 (2)
(2)
对于完全弹性碰撞,要求两个滑行器的碰撞面有用弹性良好的弹簧组成的缓冲器,我们可用钢圈作完全弹性碰撞器;对于完全非弹性碰撞,碰撞面可用尼龙搭扣、橡皮泥或油灰;一般非弹性碰撞用一般金属合金、铁等,无论哪种碰撞面,必须保证是对心碰撞。
当两滑块在水平的导轨上作对心碰撞时,忽略气流阻力,且不受其他任何水平方向的外力的影响,因此这两个滑块组成的力学系统在水平方向动量守恒。由于滑块作一维运动,式(2)中矢量 可改成标量
可改成标量 ,
,  的方向由正负号决定,若与所选取的坐标轴方向相同则取正号,反之则取负号。
的方向由正负号决定,若与所选取的坐标轴方向相同则取正号,反之则取负号。
n
完全弹性碰撞
完全弹性碰撞的标志是碰撞前后动量守恒,动能也守恒,即
 (3)
(3)
 (4)
(4)
由(3)、(4)两式可解得碰撞后的速度为
 (5)
(5)
 (6)
(6)
如果 ,则有
,则有
 (7)
(7)
 (8)
(8)
动量损失率为
 (9)
(9)
能量损失率为
 (10)
(10)
理论上,动量损失和能量损失都为零,但在实验中,由于空气阻力和气垫导轨本身的原因,不可能完全为零,但在一定误差范围内可认为是守恒的。
n
完全非弹性碰撞
碰撞后,二滑块粘在一起以同一速度运动,即为完全非弹性碰撞。在完全非弹性碰撞中,系统动量守恒,动能不守恒。
 (11)
(11)
在实验中,让 ,则有
,则有
 (12)
(12)
 (13)
(13)
动量损失率
 (14)
(14)
动能损失率
 (15)
(15)
n
一般非弹性碰撞
一般情况下,碰撞后,一部分机械能将转变为其他形式的能量,机械能守恒在此情况已不适用。牛顿总结实验结果并提出碰撞定律:碰撞后两物体的分离速度 与碰撞前两物体的接近速度成正比,比值称为恢复系数,即
与碰撞前两物体的接近速度成正比,比值称为恢复系数,即
 (16)
(16)
恢复系数 由碰撞物体的质料决定。
由碰撞物体的质料决定。 值由实验测定,一般情况下
值由实验测定,一般情况下 ,当
,当 时,为完全弹性碰撞;
时,为完全弹性碰撞; 时,为完全非弹性碰撞。
时,为完全非弹性碰撞。
n
验证机械能守恒定律
如果一个力学系统只有保守力做功,其他内力和一切外力都不做功,则系统机械能守恒。如图4.1.2-2所使,将气垫导轨一端加一垫块,使导轨与水平面成 角,把质量为
角,把质量为 的砝码用细绳通过滑轮与质量为
的砝码用细绳通过滑轮与质量为  的滑块相连,滑轮的等效质量为
的滑块相连,滑轮的等效质量为 ,根据机械能守恒定律,有
,根据机械能守恒定律,有
 (17)
(17)

式中 为砝码
为砝码 下落的距离,
下落的距离, 和
和 分贝为滑块通过
分贝为滑块通过 距离的始末速度。如果将导轨调成水平,则有
距离的始末速度。如果将导轨调成水平,则有
 (18)
(18)
在无任何非保守力对系统做功时,系统机械能守恒。但在实验中存在耗散力,如空气阻力和滑轮的摩擦力等做功,使机械能有损失,但在一定误差范围内可认为机械能是守恒的。
实验内容
n
研究三种碰撞状态下的守恒定律
l
取两滑块 、
、 ,且
,且 ,用物理天平称
,用物理天平称 、
、 ,用物理天平称
,用物理天平称 、
、 的质量(包括挡光片)。将两滑块分别装上弹簧钢圈,滑块
的质量(包括挡光片)。将两滑块分别装上弹簧钢圈,滑块 置于两光电门之间(两光电门距离不可太远),使其静止用
置于两光电门之间(两光电门距离不可太远),使其静止用 碰
碰 分别记下
分别记下 通过第一个光电门的时间
通过第一个光电门的时间 和经过第二个光电门的时间
和经过第二个光电门的时间 ,以及
,以及 通过第二个光电门的时间
通过第二个光电门的时间 ,重复五次,记录所测数据,数据表格自拟,计算
,重复五次,记录所测数据,数据表格自拟,计算 、
、 。
。
l
分别在两滑块上换上尼龙搭扣,重复上述测量和计算。
l
分别在两滑块上换上金属碰撞器,重复上述测量和结果。
n
验证机械能守恒定律
l
 时,测量
时,测量 、
、 、
、 、
、 、
、 、
、 ,计算势能增量
,计算势能增量 和动量增量
和动量增量  ,重复5次测量,数据表格自拟。
,重复5次测量,数据表格自拟。
l
 时(即将导轨一端垫起一固定高度
时(即将导轨一端垫起一固定高度  ,
, ),重复以上测量。
),重复以上测量。
设计性内容
n
用一劲度系数为K的弹簧和一质量为m的滑块,在气垫导轨上验证机械能守恒定律。
思考题
n
碰撞前后系统总动量不相等,试分析其原因。
n
恢复系数 的大小取决于哪些因素?
的大小取决于哪些因素?
n
你还能想出验证机械能守恒的其他方法吗?