国际计量局等七个国际组织于1993年指定了具有国际指导性的“测量不确定度表示指南 ISO 1993（E）” （以下简称《指南》）。几年来国际与国内的科技文献开始采用不确定度概念，我国各个高校也不断开展这方面的讨论，改革教学内容与方法，以求与国际接轨。虽然一些学者对《指南》的有些内容持批评态度[注1]，但总的趋势是在贯彻《指南》的同时，不断改善它。

测量不确定度定义为测量结果带有的一个参数，用以表征合理赋予被测量量的分散性，它是被测量客观值在某一量值范围内的一个评定。不确定度理论将不确定度按照测量数据的性质分类：符合统计规律的，称为A类不确定度，而不符合统计规律的统称为B类不确定度。测量不确定度的理论保留系统误差的概念，也不排除误差的概念。这里的误差指测量值与平均值之差或测量值与标准值（用更高级的仪器的测量值）的偏差。

测量中凡是不符合统计规律的不确定度统称为B类不确定度，记为Δ_B 。它包含了由测量者估算产生的部分Δ_估和仪器精度有限所产生的最大允差Δ_仪。Δ_仪包含了仪器的系统误差，也包含了环境以及测量者自身可能出现的变化（具随机性）对测量结果的影响。Δ_仪可从仪器说明书中得到，它表征同一规格型号的合格产品，在正常使用条件下，一次测量可能产生的最大误差。一般而言，Δ_仪为仪器最小刻度所对应的物理量的数量级（但不同仪器差别很大，一些常用仪器的最大允差见第26页）。

测量者对被测物或对仪器示数判断的不确定性会产生估算误差Δ_估。对于有刻度的仪器仪表，通常Δ_估为最小刻度的十分之几，小于Δ_仪（因为最大允差已包含了测量者正确使用仪器的估算误差）。比如，估读螺旋测微器最小刻度的十分之一为0.001毫米，小于其最大允差0.004毫米；估读钢板尺最小刻度的十分之一为0.1毫米，小于其最大允差0.15毫米。但有时Δ_估会大于Δ_仪。比如，用电子秒表测量几分钟的时间，测量者在计时判断上会有0.1-0.2秒的误差。而电子秒表的稳定性为10-5秒/天，显然仪器的最大允差小得实在可以忽略。又如第30届国际物理奥林匹克竞赛实验题中要测量一个摆杆的质心到一端的距离。将摆杆放到一个“⊥”型物上并使之平衡，测量支撑点到摆一端的距离。由于“⊥”型物棱宽为2mm ，摆杆在棱上移动±1mm均能保持平衡，使得一次测量的估算误差应为±1mm ，大于钢直尺的最大允差Δ_仪=0.15mm 。在拉伸法测金属丝杨氏模量实验中，由于难以对准金属丝被轧头夹住的位置，钢丝长度的估算误差可达±（1-2）mm 。在暗室中做几何光学实验，进行长度测量时，长度的估算误差也可达±（1-2）mm 。如果Δ_估和Δ_仪是彼此无关的，B类不确定度Δ_B为它们的合成：

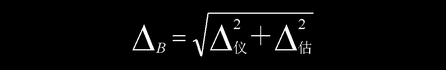
若Δ_估和Δ_仪中，某个量小于另一量的三分之一，平方后将小一个数量级，则可以忽略不计。由于一般而言，Δ_估比Δ_仪小（正常使用下已包含其中），在以下的讨论中仅以Δ_仪表示Δ_B。

多次用同一规格型号的不同仪器测量同一物理量，测量值可能不同。这些测量值与平均值之差也是按一定概率分布的。正态分布是连续型随机变量中最常用、最重要的分布。一般而言，在相同条件下大批生产的产品，其质量指标一般服从正态分布。如某个数量指标X是很多随机因素之和，而每种因素所起的作用均匀微小，则X为服从随机分布的变量。例如，工厂大量生产某一产品，当设备、技术、原材料、工艺等可控制的生产条件都相对稳定，不存在系统误差的明显因素，则产品的质量指标近似服从正态分布。如果仪器的测量误差在最大允差范围内出现的概率都相等（如长度块规在一定温度范围内由于热胀冷缩导致的长度值变化），就为均匀分布。界于两种分布之间则可用三角分布来描述。

一次测量值的B类标准差为

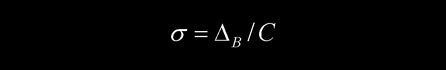
其中C称为置信系数。在最大允差范围内，对于正态分布，C=√9 =3；对于三角分布，C= √6，对于均匀分布，C=√3。第32页给出几种常用仪器的误差分布以及C的取值，见下表[注2]：

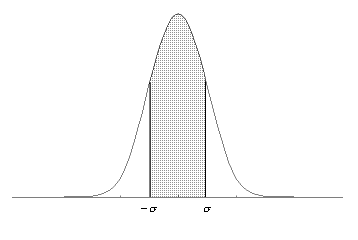
符合正态分布的测量列中某次测量值与平均值之差落在[-σ，σ]之间的概率为68.3%,落在[-2σ，2σ]之间为95.55%,落在[-3σ，3σ]之间的概率为99.73%（见图1），所以仪器的最大允差规定为Δ_仪=3σ。不同的分布，在相同范围内的置信概率有所不同。不明确这一点，在合成不确定度的A类分量和B类分量时，就无法给出正确的置信概率和置信区间。为了说明这一点，先要做一些数学铺垫。     [5]

按照概率统计理论[注3]，若x是连续型随机变量，其概率密度函数为f(x)，则其数学期望值为

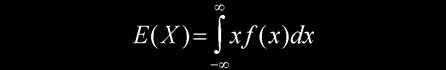
其方差为

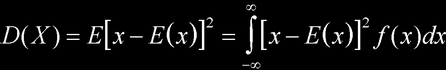
标准差为

对于等精度测量，随机量其数学期望值（即平均值）为

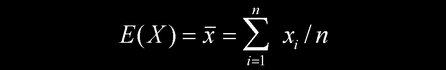
方差为

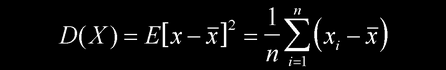
标准差为

设随机变量X在[a,b]上服从均匀分布（见图2），即

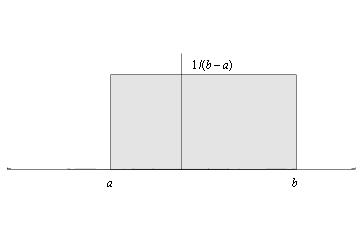
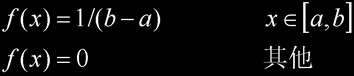
其平均值为

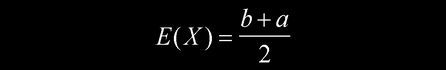
其方差为

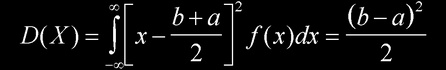
其标准差为

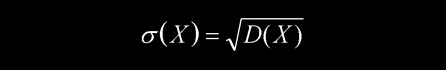
特例：当a = -Δ_仪 ,b =Δ_仪时，σ(X)=Δ_仪/√3 ≈0.577Δ_仪。也即如果仪器误差符合均匀分布，其一次测量值与标准值之差落在[-σ，σ]内的概率为57.7%，低于正态分布相应的68.3%；而落在[-√3σ，√3σ]内的概率就已经达到100%，与正态分布有很大不同（比较图1和图2）。

设随机变量X在[-Δ_仪 ,Δ_仪]上的分布为三角分布（见图3）

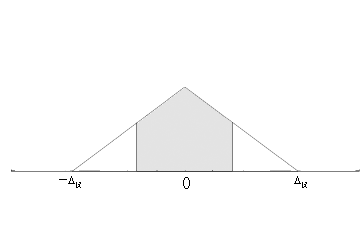
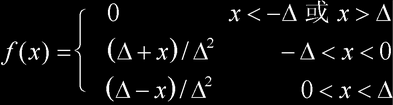
由其对称性易得测量列的平均值为

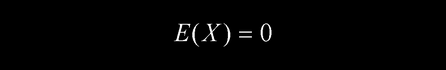
方差为

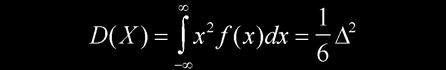
标准差

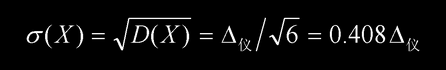
X落在[-σ, σ]之间的概率P（σ），如图3中阴影的面积，P（σ）=0.758；而 P（2σ）=0.966。三种分布的标准差以及各置信区间相应的概率如下表：

因此，不能笼统地说测量误差落在标准差范围内的概率为68.3%，落在两倍标准差范围内的概率为95.5%。在合成标准不确定度时，要注意区分不同的分布。     [5]

将A类和B类标准差合成得到置信概率P=0.68的合成标准不确定度：

若考虑到测量次数，还应t因子修正。将合成标准不确定度乘以一个与一定置信概率相联系的包含因子（或称覆盖因子）K，得到增大置信概率的不确定度叫做展伸不确定度（或扩展不确定度）。通常取置信概率为0.95，K=2。对正态分布，k_0.95=1.96 ≈ K=2。这时的展伸不确定度为

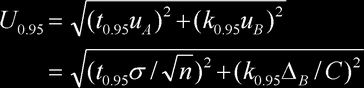
考虑到通常测量6次左右,查阅t因子表，t_0.95=2.57, t²/6≈1,C=3, K≈k_0.95=1.96,(K/C)≈0.5。所以，置信概率P=0.95的展伸不确定度的便于操作的公式为

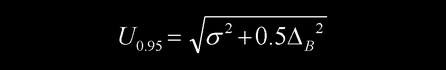
用均匀分布或三角分布得到的B类标准不确定度与服从正态分布的A类标准不确定度来计算合成不确定度时，要用到卷积运算，其结果和σ与Δ_仪之比有关，可参阅[文献4]。注意到不确定度的统计学意义和在上述操作中的近似，在实际工作中，常常忽略不同分布的差别（有时也不知道是什么分布），而把Δ_仪 当成均匀分布，取置信因子C=√3。这样得到一种较为保守的公式

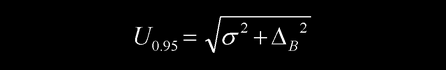
其置信概率应记为P≥0.95。     [5]

在研究两个物理量之间的关系时，常用到作图法。在作图法中，一对测量值确定一个点，叫做“数据点”（教材第一册43页）。如果在作图时用线段标示出测量值的不确定度±Δ_仪，则将会更全面地反映出实验的精度。线段的长度为2Δ_仪，这种小线段称为误差杆。考虑到通常选比较容易测量的物理量作为自变量，常用横坐标表示之，且其Δ仪较小，所以在作图中往往只需沿纵坐标方向画出误差杆。如果绝大多数数据点可以拟合成一条直线（或曲线），只有一个点偏离甚远，就要考虑这一对测量值的可靠性了。严格地讲，应该重新测量。但有时无法或没必要重做实验，可不可以舍弃这个点呢？一般来说，在有限范围内，两个物理量之间的关系多为连续的；反映其关系的曲线不大可能有大的突然起伏。我们可以参照测量不确定度理论中剔除坏值的3σ原则来处理。如果该点到按其他点拟合的曲线的距离大于1.5倍误差杆的长度，就可以舍弃该点。不画出误差杆就难以判断。要注意，曲线拟合是对多个数据点的统计学意义下的操作，若一共只有3、4个点，就不能草率地舍弃任何一个点了。

还要注意，各个数据点的误差杆长度不一定相等。或者，对数据做某种处理（如取对数）后，再进行作图，误差杆的长度也会变化。譬如，某1.0级的电压表的量程为100伏，对于测量值为20.0伏、30.0伏、40.0伏和 50.0伏，它们的最大允差均为±1.0伏。若纵坐标为电压，则误差杆的长度都是2×0.1伏；而若以电压值的对数为纵坐标，则误差杆的长度为2×ΔV/V=0.2/V，电压值不同，误差杆长度就不同。

作图法的最大优点是直观。在诸多数据点的拟合中，如果发现有一个点明显偏离所拟合的曲线，就需要在这个点所处物理条件附近，再进行仔细的实验，查明是否是实验误差，还是有新的现象或规律。但作图法需较长时间，曲线拟合过程中会引入误差；求解实验方程参数及其不确定度比较麻烦。用回归法只需按动计算器的几个键，就可以确定实验方程的参数及其不确定度。但如果实验数据有误，或所拟合的方程形式不合适，则相关系数小，必须重新检查数据或方程形式，由于不直观，一时难以断定问题之所在。

若数据点可以拟合为一条直线，线性方程的一般形式为

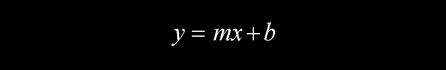
数据为Xi和Yi,每次测量的最大允差为ΔXi和ΔYi，i = 1,2,…,n。拟合直线的斜率m的相对不确定度为

*

式中

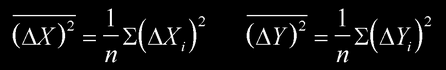
分别为相应测量值最大允差的平方平均值。

截距的不确定度为

**

概率论给出回归法线性拟合的斜率的标准差为

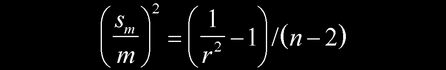
式中n 为X（或Y）的测量数据个数，r为相关系数。

截距的标准差为

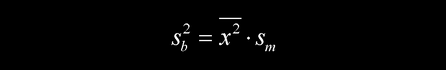
如果两组物理量之间的关系确实为线性，按 * 和 ** 式由各个测量值最大允差计算得到的和一般大于由回归法计算得到的结果。前者只考虑每次测量值的仪器最大允差，而不考虑各个数据点对于所拟合的直线的偏离情况（线性拟合的程度由眼睛直观判断）。而回归法则相反，不考虑每次测量值的仪器最大允差，只考虑各个数据点对于所拟合的线性关系的偏离情况。线性拟合程度的“好坏”由相关系数给出。如果测量值中有一个“坏值”，由于作图法能直观察觉，方便作出相应处理（剔除坏值或重做实验改正错误）。而回归法则是根据所有数据计算，一个错误数据也可能使相关系数严重减小。这时难以判断是整体线性不好，还是个别数据出了差错。两全的办法是先画出图来，直观判断线性好坏。如果确定线性关系，再用计算器按键操作，很方便地求出线性方程的斜率和截距以及它们的标准差，不必按公式详细计算。

对于不是线性关系的物理规律，拟合曲线比较麻烦；由曲线求解实验方程的参数也比较困难。有时可以对物理量进行适当变换，按变换后的的物理量作图，把曲线改成直线，就方便处理了。现在，很多商品计算器对于线性、对数、指数和幂函数关系都具有回归计算功能，只需按相应的键就可以拟合这些函数关系。实验数据处理方法也应“与时俱进”，充分享用新技术带给人类的方便。有必要让我们的学生掌握这些方法。     [5]